题目内容
3.与双曲线$\frac{x^2}{5}$-$\frac{y^2}{4}$=-1有相同焦点,且离心率为$\frac{3}{5}$的椭圆方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{25}=1$.分析 求出椭圆的焦点坐标,利用离心率求出a、c、b,即可得到椭圆的标准方程.
解答 解:双曲线$\frac{x^2}{5}$-$\frac{y^2}{4}$=-1的焦点坐标(0,-3),(0,3),则椭圆的焦点坐标为(0,-3),(0,3),
c=3,离心率为$\frac{3}{5}$,a=5,则b=4,与双曲线$\frac{x^2}{5}$-$\frac{y^2}{4}$=-1有相同焦点,且离心率为$\frac{3}{5}$的椭圆方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{25}=1$
故答案为:$\frac{x^2}{16}+\frac{y^2}{25}=1$.
点评 本题考查椭圆的简单性质,双曲线的简单性质的应用,注意双曲线的焦点坐标的位置,考查计算能力.

练习册系列答案
相关题目
20.已知函数f(x)的部分图象如图,则f(x)的解析式可能为( )
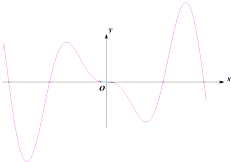

| A. | f(x)=xcosx-sinx | B. | f(x)=xsinx | C. | f(x)=xcosx+sinx | D. | f(x)=xcosx |
18.用反证法证明命题“若a+b=1,则a,b至少有一个不比1大时,”首先假设( )
| A. | a,b都小于等于1 | B. | a,b都大于1 | ||
| C. | a,b都大于等于1 | D. | a,b都小于1当a<0时 |
12.“金能导电,银能导电,铜能导电,铁能导电,所有一切金属都能导电.”此推理方法是( )
| A. | 归纳推理 | B. | 类比推理 | C. | 演绎推理 | D. | 以上均有可能 |
 将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),
将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),