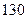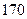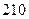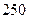题目内容
已知函数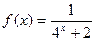 ,数列
,数列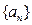 通项公式
通项公式
为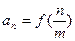
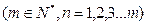
数列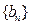 满足
满足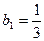 ,
,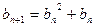 ,设
,设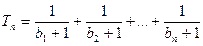
(1)证明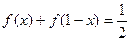 ,并求数列
,并求数列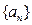 前
前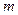 项和
项和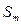
(2)若(1)中的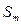 满足对任意不小于2的正整数
满足对任意不小于2的正整数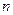 ,
,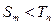 恒成立,求
恒成立,求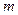 最大值
最大值
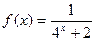 ,数列
,数列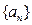 通项公式
通项公式为
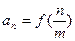
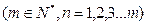
数列
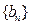 满足
满足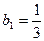 ,
,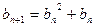 ,设
,设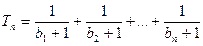
(1)证明
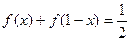 ,并求数列
,并求数列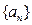 前
前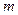 项和
项和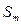
(2)若(1)中的
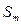 满足对任意不小于2的正整数
满足对任意不小于2的正整数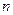 ,
,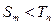 恒成立,求
恒成立,求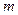 最大值
最大值(1)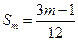 (2)5
(2)5
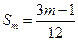 (2)5
(2)5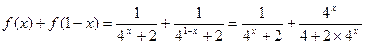
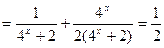
所以
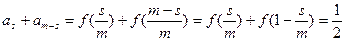
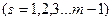
所以
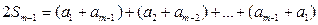
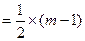
所以
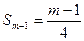 ,
,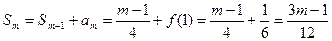
(2)
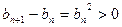 ,所以
,所以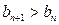 ,数列
,数列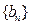 为单调递增数列,所以
为单调递增数列,所以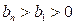
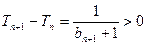 所以
所以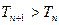 ,即数列
,即数列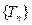 为单调递增数列,
为单调递增数列,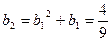
且
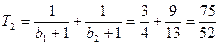 ,
,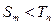 对任意的不小于
对任意的不小于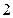 的正整数恒成立
的正整数恒成立所以
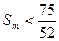 ,即
,即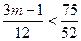 ,解得
,解得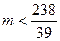 ,所以
,所以 最大值为
最大值为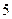

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
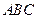 中,
中,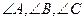 所对的边分别为
所对的边分别为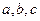 ,满足
,满足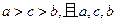 成等差数列,
成等差数列,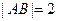 ,求点
,求点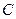 的轨迹方程.
的轨迹方程.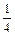 .
.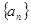 中,
中,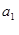 =1,
=1,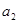 ="3+5,"
="3+5," 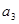 =7+9+11,
=7+9+11,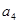 =13+15+17+19,…,则
=13+15+17+19,…,则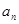 = .
= . 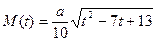 (其中
(其中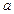 为鱼苗成本,
为鱼苗成本,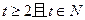 )。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。
)。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。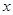 ,以后每次生成的结果是将上一次生成的每一个数
,以后每次生成的结果是将上一次生成的每一个数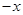 ,另一个是
,另一个是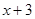 .设第
.设第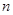 次生成的数的个数为
次生成的数的个数为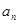 ,
,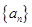 的前
的前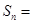 ;若
;若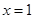 ,前
,前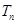 ,则
,则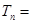 .
.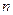 边形的内角的度数成等差数列,若公差是
边形的内角的度数成等差数列,若公差是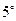 ,且最大角是
,且最大角是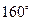 ,则
,则
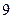
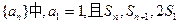 成等差数列
成等差数列 ,则
,则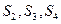 分别为 ,由此猜想出
分别为 ,由此猜想出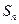 = 。
= 。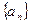 的前
的前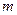 项的和为
项的和为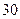 ,前
,前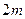 项的和为
项的和为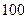 ,则它的前
,则它的前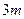 项的和为( )
项的和为( )