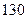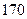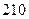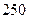题目内容
在等比数列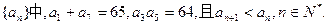
(1)求数列{an}的通项公式;
(2)求数列{an}的前5项的和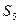
(3)若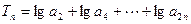 ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值.
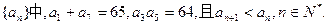
(1)求数列{an}的通项公式;
(2)求数列{an}的前5项的和
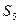
(3)若
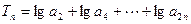 ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值.(1)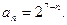 (2)
(2)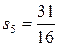 (3)当n = 3时,Tn的最大值为9lg2
(3)当n = 3时,Tn的最大值为9lg2
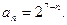 (2)
(2)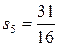 (3)当n = 3时,Tn的最大值为9lg2
(3)当n = 3时,Tn的最大值为9lg2(1)设数列{an}的公比为q. 由等比数列性质可知:
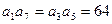 , 而
, 而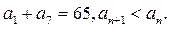
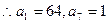 , ------------------------3 分
, ------------------------3 分
由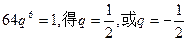 (舍), -------------- 5 分
(舍), -------------- 5 分
故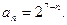 --------------------7 分
--------------------7 分
(2)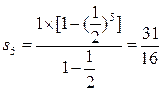 -------------9 分
-------------9 分
(3)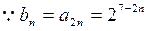
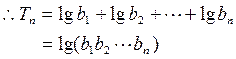 -------------------10
-------------------10
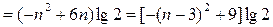 ---------------12 分
---------------12 分
∴当n = 3时,Tn的最大值为9lg2. --------------------14分
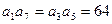 , 而
, 而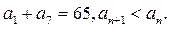
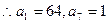 , ------------------------3 分
, ------------------------3 分 由
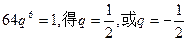 (舍), -------------- 5 分
(舍), -------------- 5 分故
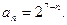 --------------------7 分
--------------------7 分 (2)
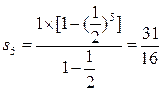 -------------9 分
-------------9 分(3)
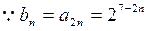
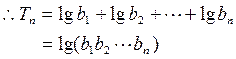 -------------------10
-------------------10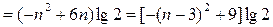 ---------------12 分
---------------12 分∴当n = 3时,Tn的最大值为9lg2. --------------------14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
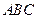 中,
中,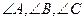 所对的边分别为
所对的边分别为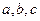 ,满足
,满足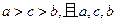 成等差数列,
成等差数列,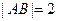 ,求点
,求点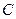 的轨迹方程.
的轨迹方程.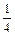 .
.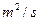 的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2
的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2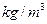 和0.2
和0.2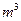 的水量,即从A股流入B股100
的水量,即从A股流入B股100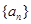 中,
中,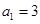 且对于任意大于
且对于任意大于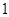 的正整数
的正整数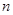 ,点
,点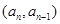 在直线
在直线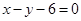 上,则
上,则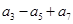 的值为( ).
的值为( ).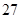
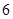
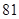
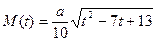 (其中
(其中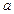 为鱼苗成本,
为鱼苗成本,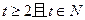 )。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。
)。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。 ,最长年限为10年,可以分期付款,张先生根据自己的实际情况估计每年最多可偿还5000元,打算平均10年还清,如果银行贷款按复利计算,那么张先生最大限额的贷款是多少元?(
,最长年限为10年,可以分期付款,张先生根据自己的实际情况估计每年最多可偿还5000元,打算平均10年还清,如果银行贷款按复利计算,那么张先生最大限额的贷款是多少元?(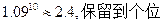 )
)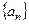 的前
的前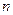 项和
项和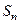 满足
满足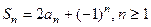 .
.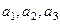 ;
;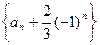 为等比数列,并求出
为等比数列,并求出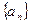 的前
的前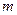 项的和为
项的和为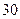 ,前
,前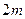 项的和为
项的和为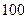 ,则它的前
,则它的前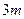 项的和为( )
项的和为( )