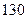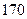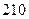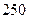题目内容
在各项均为正数的数列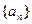 中,前
中,前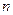 项和
项和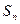 满足
满足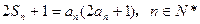 。
。
(1)证明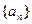 是等差数列,并求这个数列的通项公式及前
是等差数列,并求这个数列的通项公式及前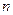 项和的公式;
项和的公式;
(2)在平面直角坐标系 面上,设点
面上,设点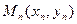 满足
满足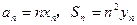 ,且点
,且点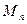 在直线
在直线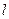 上,
上,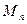 中最高点为
中最高点为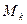 ,若称直线
,若称直线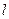 与
与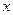 轴、直线
轴、直线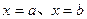 所围成的图形的面积为直线
所围成的图形的面积为直线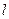 在区间
在区间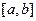 上的面积,试求直线
上的面积,试求直线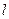 在区间
在区间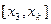 上的面积;
上的面积;
(3)若存在圆心在直线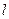 上的圆纸片能覆盖住点列
上的圆纸片能覆盖住点列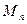 中任何一个点,求该圆纸片最小面积.
中任何一个点,求该圆纸片最小面积.
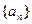 中,前
中,前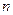 项和
项和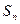 满足
满足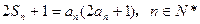 。
。(1)证明
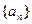 是等差数列,并求这个数列的通项公式及前
是等差数列,并求这个数列的通项公式及前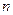 项和的公式;
项和的公式;(2)在平面直角坐标系
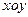 面上,设点
面上,设点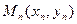 满足
满足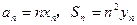 ,且点
,且点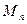 在直线
在直线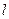 上,
上,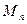 中最高点为
中最高点为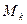 ,若称直线
,若称直线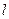 与
与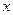 轴、直线
轴、直线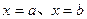 所围成的图形的面积为直线
所围成的图形的面积为直线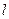 在区间
在区间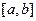 上的面积,试求直线
上的面积,试求直线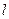 在区间
在区间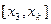 上的面积;
上的面积;(3)若存在圆心在直线
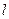 上的圆纸片能覆盖住点列
上的圆纸片能覆盖住点列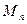 中任何一个点,求该圆纸片最小面积.
中任何一个点,求该圆纸片最小面积.(1)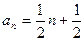
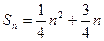 (2)
(2)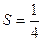 (3)
(3)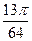
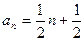
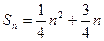 (2)
(2)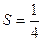 (3)
(3)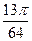
(1)由已知得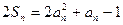 ①
①
故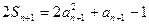 ②
②
②-①得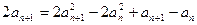
结合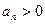 ,得
,得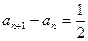
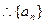 是等差数列 ……(2分)
是等差数列 ……(2分)
又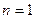 时,
时,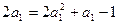 ,解得
,解得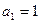 或
或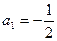
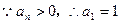
又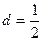 ,故
,故
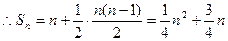 ……(4分)
……(4分)
(2)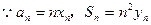
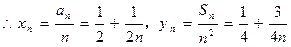
即得点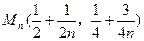
设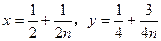 ,消去n,得
,消去n,得
即直线C的方程为 ……(7分)
……(7分)
又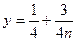 是n的减函数
是n的减函数
∴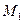 为
为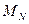 中的最高点,且
中的最高点,且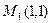
又M3的坐标为(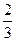 ,
,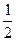 )
)
∴C与x轴、直线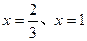 围成的图形为直角梯形
围成的图形为直角梯形
从而直线C在[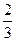 ,1]上的面积为
,1]上的面积为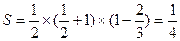 ……(9分)
……(9分)
(3)由于直线C: 上的点列Mn依次为
上的点列Mn依次为
M1(1,1),M2(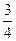 ,
,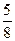 ),M3(
),M3(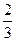 ,
,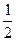 ),……,Mn(
),……,Mn(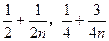 ),
),
而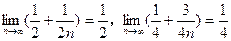
因此,点列Mn沿直线C无限接近于极限点M(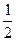 ,
,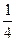 ) ……(12分)
) ……(12分)
又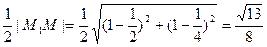
所以最小圆纸片的面积为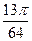 ……(14分)
……(14分)
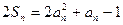 ①
①故
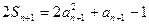 ②
②②-①得
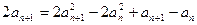
结合
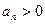 ,得
,得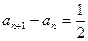
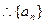 是等差数列 ……(2分)
是等差数列 ……(2分)又
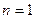 时,
时,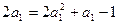 ,解得
,解得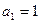 或
或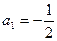
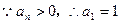
又
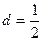 ,故
,故
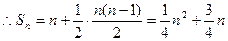 ……(4分)
……(4分)(2)
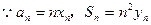
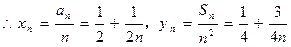
即得点
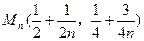
设
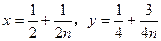 ,消去n,得
,消去n,得
即直线C的方程为
 ……(7分)
……(7分)又
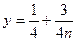 是n的减函数
是n的减函数∴
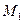 为
为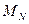 中的最高点,且
中的最高点,且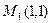
又M3的坐标为(
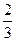 ,
,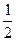 )
)∴C与x轴、直线
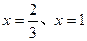 围成的图形为直角梯形
围成的图形为直角梯形从而直线C在[
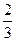 ,1]上的面积为
,1]上的面积为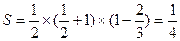 ……(9分)
……(9分)(3)由于直线C:
 上的点列Mn依次为
上的点列Mn依次为M1(1,1),M2(
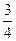 ,
,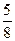 ),M3(
),M3(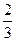 ,
,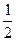 ),……,Mn(
),……,Mn(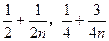 ),
),而
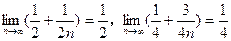
因此,点列Mn沿直线C无限接近于极限点M(
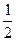 ,
,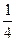 ) ……(12分)
) ……(12分)又
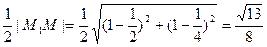
所以最小圆纸片的面积为
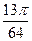 ……(14分)
……(14分)
练习册系列答案
相关题目
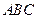 中,
中,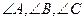 所对的边分别为
所对的边分别为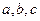 ,满足
,满足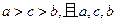 成等差数列,
成等差数列,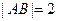 ,求点
,求点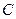 的轨迹方程.
的轨迹方程.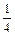 .
.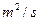 的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2
的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2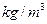 和0.2
和0.2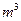 的水量,即从A股流入B股100
的水量,即从A股流入B股100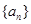 中,
中,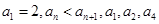 成等比数列,则
成等比数列,则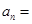 ______ _______.
______ _______.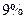 ,最长年限为10年,可以分期付款,张先生根据自己的实际情况估计每年最多可偿还5000元,打算平均10年还清,如果银行贷款按复利计算,那么张先生最大限额的贷款是多少元?(
,最长年限为10年,可以分期付款,张先生根据自己的实际情况估计每年最多可偿还5000元,打算平均10年还清,如果银行贷款按复利计算,那么张先生最大限额的贷款是多少元?(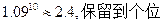 )
)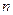 边形的内角的度数成等差数列,若公差是
边形的内角的度数成等差数列,若公差是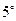 ,且最大角是
,且最大角是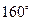 ,则
,则
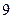
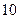
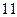
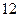
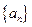 和
和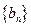 的前
的前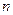 项和分别为
项和分别为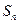 和
和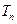 ,且
,且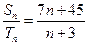 ,则使得
,则使得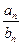 为整数的正整数
为整数的正整数 的前
的前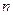 项之和
项之和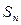 满足
满足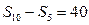 ,
,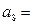 .
.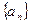 的前
的前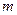 项的和为
项的和为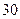 ,前
,前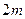 项的和为
项的和为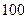 ,则它的前
,则它的前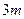 项的和为( )
项的和为( )