题目内容
【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
【答案】(1)f(x)在0<x≤1上,函数为减函数;在x>1上,函数为增函数;(2)a≤4.
【解析】试题分析:(1)将条件带入求导,得![]() =x-
=x-![]() ,进而根据导数的正负可得函数的单调性;
,进而根据导数的正负可得函数的单调性;
(2)令H(x)= f(x)-(x3+4x-lnx)= -x3+![]() x2-4x=x(-x2+ax-4)所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,即x(-x2+ax-4) ≤0在x>0上恒成立,进而转化为-x2+ax-4≤0在x>0上恒成立,进而可得解.
x2-4x=x(-x2+ax-4)所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,即x(-x2+ax-4) ≤0在x>0上恒成立,进而转化为-x2+ax-4≤0在x>0上恒成立,进而可得解.
试题解析:
(1)、当a=![]() 时,f(x)=
时,f(x)=![]() x2-lnx,
x2-lnx, ![]() =x-
=x-![]()
令导函数等于0,解得x=1或x=-1(舍),
所以当![]() >0时,x>1,当
>0时,x>1,当![]() <0,0<x<1
<0,0<x<1
所以f(x)在0<x≤1上,函数为减函数;在x>1上,函数为增函数。
(2)令H(x)= f(x)-(x3+4x-lnx)= -x3+![]() x2-4x=x(-x2+ax-4)
x2-4x=x(-x2+ax-4)
所以要使f(x)≤x3+4x-lnx,在定义域内恒成立,只需H(x)≤0,在定义域内恒成立,
即x(-x2+ax-4) ≤0在x>0上恒成立。
由于x>0,所以只要-x2+ax-4≤0在x>0上恒成立
所以应满足△≤0或者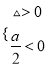 ,所以a≤4.
,所以a≤4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.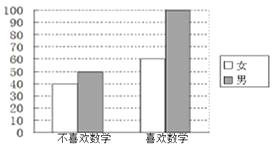
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?