题目内容
(本小题满分12分)已知函数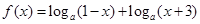 ,
,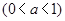
(I)求函数 的定义域;
的定义域;
(II)若函数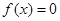 ,求
,求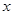 的值;
的值;
(III)若函数 的最小值为
的最小值为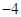 ,求
,求 的值.
的值.
(1)(-3,1).(2)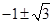 .(3)
.(3)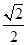 .
.
解析试题分析: (I)由对数的真数大于零可得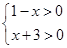 ,从而得到函数的定义域.
,从而得到函数的定义域.
(II)根据先根据对数的运算法则得到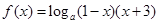 ,再由f(x)=0,得
,再由f(x)=0,得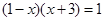 ,解此方程可得x值,要注意验证是否在定义域内.
,解此方程可得x值,要注意验证是否在定义域内.
(III)先利用对数的运算法则把f(x)化简为 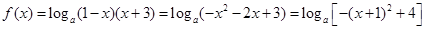 ,
,
因为真数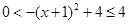 ,再根据
,再根据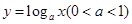 在定义域内是减函数,从而可得
在定义域内是减函数,从而可得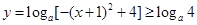 ,因而
,因而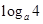 =-4,解此对数方程可得a的值.
=-4,解此对数方程可得a的值.
(1)要使函数有意义:则有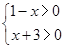 ,解之得:
,解之得: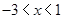 ,
,
所以函数的定义域为:(-3,1).……………………………………………4分
(2)函数可化为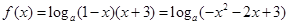 , 由
, 由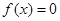 ,得
,得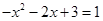 ,
,
即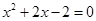 ,
,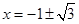 ;…………………………………………6分
;…………………………………………6分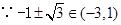 ,
,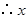 的值是
的值是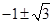 .…………………………8分
.…………………………8分
(3)函数可化为: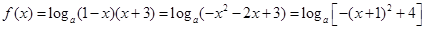 ,
,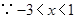
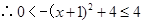 ;……………………………………………9分
;……………………………………………9分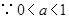 ,
,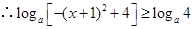 ,即
,即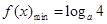 ;…………10分
;…………10分
由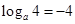 ,得
,得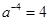 ,
,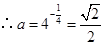 .………………………………12分
.………………………………12分
考点:对数函数的定义域,值域,对数的运算法则, 对数方程及不等式的解法.
点评:掌握对数函数的定义域,值域,单调性是研究此类问题的前提,一般地说: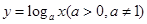 ,其定义域为
,其定义域为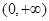 ,值域为R,当a>1时,对数函数是增函数;
,值域为R,当a>1时,对数函数是增函数;
当0<a<1时,对数函数是减函数。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
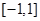 上的奇函数
上的奇函数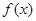 ,当
,当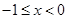 时,
时,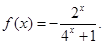
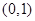 上的单调性,并给予证明;
上的单调性,并给予证明;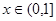 时,关于
时,关于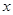 的方程
的方程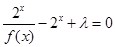 有解,试求实数
有解,试求实数 的取值范围.
的取值范围.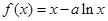 ,
,
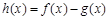 ,求函数
,求函数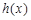 的单调区间;
的单调区间;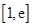 (
(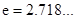 )上存在一点
)上存在一点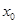 ,使得
,使得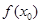
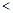
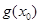 成立,求
成立,求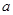 的取值范围.
的取值范围. (
(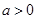 ),
),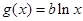 .
.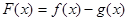 ,讨论
,讨论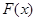 的单调性;
的单调性; 的不等式
的不等式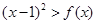 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数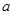 的取值范围;
的取值范围; 与
与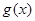 定义域上的任意实数
定义域上的任意实数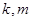 ,使得
,使得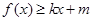 和
和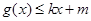 都成立,则称直线
都成立,则称直线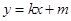 为函数
为函数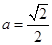 ,
,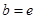 ,试探究
,试探究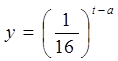 (a为常数),
(a为常数),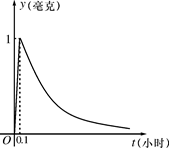
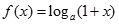 ,
,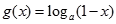 ,
,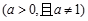 .
.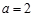 ,函数
,函数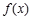 的定义域为
的定义域为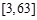 ,求函数
,求函数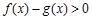 的
的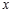 的取值范围.
的取值范围.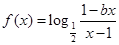 为奇函数,
为奇函数,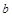 为常数.
为常数.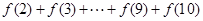 的值;
的值;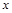 的值,不等式
的值,不等式 >
>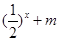 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 为定义在
为定义在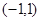 上的奇函数,当
上的奇函数,当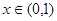 时,
时,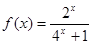 ;
;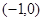 上的单调性,并给出证明.
上的单调性,并给出证明.