题目内容
(本小题满分14分)设函数 (
(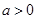 ),
),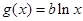 .
.
(Ⅰ)令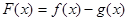 ,讨论
,讨论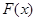 的单调性;
的单调性;
(Ⅱ)关于 的不等式
的不等式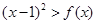 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数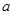 的取值范围;
的取值范围;
(Ⅲ)对于函数 与
与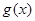 定义域上的任意实数
定义域上的任意实数 ,若存在常数
,若存在常数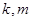 ,使得
,使得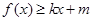 和
和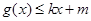 都成立,则称直线
都成立,则称直线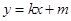 为函数
为函数 与
与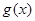 的“分界线”.设
的“分界线”.设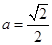 ,
,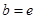 ,试探究
,试探究 与
与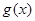 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
(Ⅰ)函数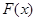 在
在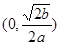 上是单调递减;在
上是单调递减;在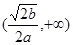 上是单调递增.
上是单调递增.
(2)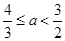 (3)
(3)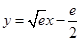 .
.
解析试题分析:(I)直接求导,利用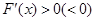 得到F(x)的单调增(减)区间;
得到F(x)的单调增(减)区间;
(II)不等式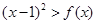 的解集中的整数恰有3个,等价于
的解集中的整数恰有3个,等价于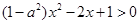 恰有三个整数解,故
恰有三个整数解,故 ,令
,令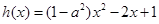 ,因为h(x)的一个零点区间为(0,1),
,因为h(x)的一个零点区间为(0,1),
所以得到另一个零点一定在区间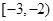 ,故
,故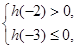 ,问题到此得解.
,问题到此得解.
(III)由(I)知可知F(x)的最小值为0,则f(x)与g(x)的图像在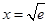 处有公共点
处有公共点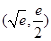 .
.
如果f(x)与g(x)存在分界线,因为方程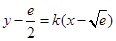 即
即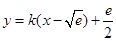 ,所以由题意可转化为
,所以由题意可转化为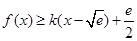 在
在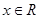 恒成立问题解决.
恒成立问题解决.
(Ⅰ)由 得:
得: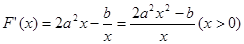 ················· 1分
················· 1分 ①当
①当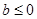 时,
时,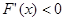 ,则函数
,则函数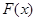 在
在 上是单调递增;····· 3分
上是单调递增;····· 3分
②当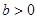 时,则当
时,则当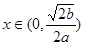 时,
时,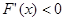 , 当
, 当 时,
时,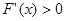
故函数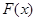 在
在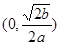 上是单调递减;在
上是单调递减;在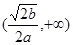 上是单调递增. ···· 5分
上是单调递增. ···· 5分
(Ⅱ)解法一:不等式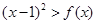 的解集中的整数恰有3个,
的解集中的整数恰有3个,
等价于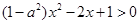 恰有三个整数解,故
恰有三个整数解,故 ,
,
令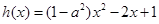 ,由
,由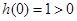 且
且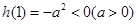 ,
,
所以函数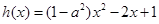 的一个零点在区间
的一个零点在区间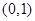 ,
,
则另一个零点一定在区间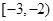 ,故
,故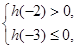 解之得
解之得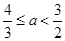 .··· 9分
.··· 9分
下面证明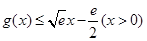 恒成立.
恒成立.
设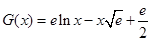 ,则
,则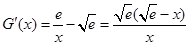 .
.
所以当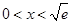 时,
时,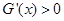 ;当
;当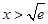 时,
时,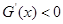 .
.
因此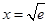 时
时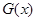 取得最大值
取得最大值 ,则
,则 成立.
成立.
故所求“分界线”方程为: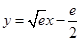 . …………14分
. …………14分
考点: 利用导数研究函数的单调性,函数的最值,函数的零点,不等式恒成立问题,分析问题解决问题的能力,推理与论证能力.
点评:本题综合性难度大,第(II)问的关键是构造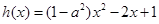 之后,判定一个零点在区间(0,1),另一个零点
之后,判定一个零点在区间(0,1),另一个零点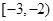 ,从而问题得解.
,从而问题得解.
第(III)问关键是理解f(x)与g(x)存在分界线,因为方程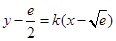 即
即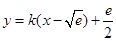 ,题目可转化为
,题目可转化为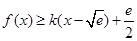 在
在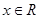 恒成立问题解决.
恒成立问题解决.

 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足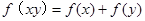 ,
, 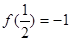
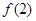 =1 (2) 求不等式
=1 (2) 求不等式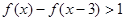 的解集.
的解集. 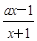 ,其中a∈R.
,其中a∈R.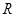 的函数
的函数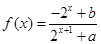 是奇函数。
是奇函数。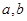 的值;
的值;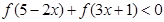
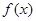 =
=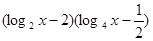 ,2≤
,2≤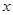 ≤4
≤4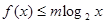 对于
对于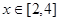 恒成立,求
恒成立,求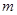 的取值范围.
的取值范围. 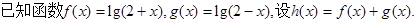
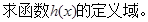
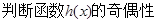 ,并说明理由.
,并说明理由.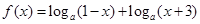 ,
,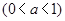
 的定义域;
的定义域;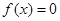 ,求
,求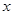 的值;
的值;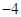 ,求
,求 的值.
的值. 的函数
的函数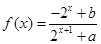 是奇函数.
是奇函数.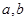 的值;
的值;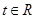 ,不等式
,不等式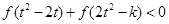 恒成立,求
恒成立,求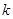 的取值范围.
的取值范围.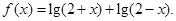
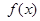 的定义域;
的定义域;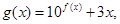 求函数
求函数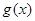 的值域.
的值域.