题目内容
(本小题满分12分) 已知函数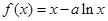 ,
,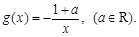
(1)设函数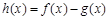 ,求函数
,求函数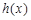 的单调区间;
的单调区间;
(2)若在区间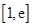 (
(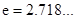 )上存在一点
)上存在一点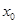 ,使得
,使得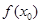
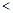
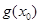 成立,求
成立,求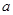 的取值范围.
的取值范围.
(1)
(2)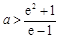 或
或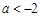 .
.
解析试题分析:(1)先求出函数h(x)的导函数,分情况讨论让其大于0求出增区间,小于0求出减区间即可得到函数的单调区间;
(2)先把f(x0)<g(x0)成立转化为h(x0)<0,即函数h(x)=x+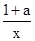 -alnx在[1,e]上的最小值小于零;再结合(Ⅱ)的结论分情况讨论求出其最小值即可求出a的取值范围
-alnx在[1,e]上的最小值小于零;再结合(Ⅱ)的结论分情况讨论求出其最小值即可求出a的取值范围
在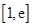 上存在一点
上存在一点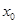 ,使得
,使得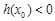 ,即
,即
函数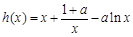 在
在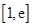 上的最小值小于零. …由(Ⅱ)可知
上的最小值小于零. …由(Ⅱ)可知
①即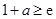 ,即
,即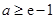 时,
时,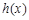 在
在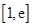 上单调递减,
上单调递减,
所以 的最小值为
的最小值为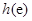 ,由
,由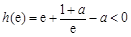 可得
可得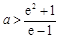 ,
,
因为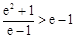 ,所以
,所以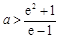 ;
;
②当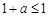 ,即
,即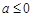 时,
时,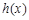 在
在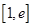 上单调递增,
上单调递增,
所以 最小值为
最小值为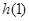 ,由
,由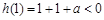 可得
可得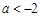 ;③当
;③当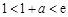 ,即
,即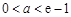 时, 可得
时, 可得 最小值为
最小值为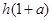 ,
,
因为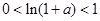 ,所以,
,所以,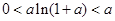
故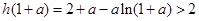
此时,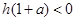 不成立.
不成立.
综上讨论可得所求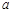 的范围是:
的范围是: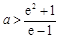 或
或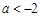 .
.
考点:本试题主要考查了利用导函数来研究函数的极值.
点评:解决该试题的关键是利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值。

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
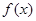 是定义在
是定义在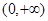 上的增函数,且对一切
上的增函数,且对一切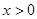 满足
满足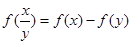 .
.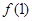 的值;
的值;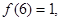 解不等式
解不等式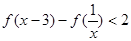 .
.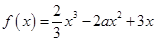 (
(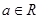 ).
).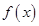 的单调区间;
的单调区间;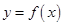 在
在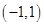 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.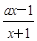 ,其中a∈R.
,其中a∈R.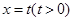 左侧的图形的面积为
左侧的图形的面积为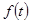 。试求函数
。试求函数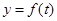 的图象.
的图象.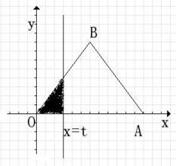
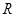 的函数
的函数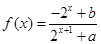 是奇函数。
是奇函数。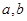 的值;
的值;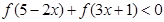
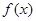 =
=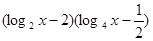 ,2≤
,2≤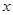 ≤4
≤4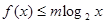 对于
对于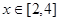 恒成立,求
恒成立,求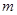 的取值范围.
的取值范围. 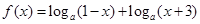 ,
,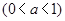
 的定义域;
的定义域;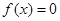 ,求
,求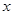 的值;
的值; ,求
,求 的值.
的值.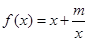 ,且
,且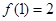
 的奇偶性,并证明;
的奇偶性,并证明;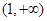 上的单调性,并用定义证明;
上的单调性,并用定义证明;
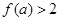 ,求
,求 的取值范围。
的取值范围。