题目内容
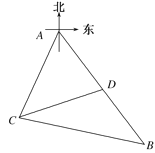
【题目】某观测站
在目标
的南偏西
方向，从
出发有一条南偏东
走向的公路，在
处测得与
相距
的公路
处有一个人正沿着此公路向
走去，走
到达
，此时测得
距离为
，若此人必须在
分钟内从
处到达
处，则此人的最小速度为( )
A. 
B. 
C. 
D. 
【答案】B
【解析】由已知得∠CAB＝25°＋35°＝60°，BC＝31，CD＝21，BD＝20，可得
，那么
，
于是在△ABC中， 
＝24，
在△ABC中，BC2＝AC2＋AB2－2AC·ABcos60°，即312＝242＋AB2－24AB，解得AB＝35或AB＝－11(舍去)，因此AD＝AB－BD＝35－20＝15.
故此人在D处距A处还有15 km，若此人必须在20分钟，即
小时内从D处到达A处，则其最小速度为15÷
＝45(km/h)．
故选B.
练习册系列答案
相关题目
【题目】已知某观光海域AB段的长度为3百公里，一超级快艇在AB段航行，经过多次试验得到其每小时航行费用Q（单位：万元）与速度v（单位：百公里／小时）（0≤v≤3）的以下数据：
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系，现有以下三种函数模型供选择：Q＝av3＋bv2＋cv，Q＝0．5v＋a，Q＝klogav＋b．
（1）试从中确定最符合实际的函数模型，并求出相应的函数解析式；
（2）该超级快艇应以多大速度航行才能使AB段的航行费用最少？并求出最少航行费用．
