Question

【题目】已知椭圆的离心率为，且过点.

（1）求椭圆方程；

（2）设不过原点的直线，与该椭圆交于两点，直线的斜率依次为，满足，试问：当变化时，是否为定值？若是，求出此定值，并证明你的结论；若不是请说明理由.

Answer 1

【答案】（1）；（2）是定值，

【解析】

试题分析：（1）求椭圆的标准方程，就是要确定的值，只要找到两个关于的等式即可，本题中一个离心率，一个是椭圆过已知点，由此可得；（2）设交点，，把直线方程与椭圆方程联立方程组，消去后，可得，计算，化简后并把代入可得结论．

试题解析：（1）依题意可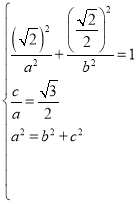得 解得.

所以椭圆的方程是.

（2）当变化时，为定值，证明如下：

由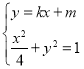得，.

设，，则， （*）

∵直线的斜率依次为，且，

∴，得，

将（*）代入得：，

经检验满足