题目内容
【题目】变量![]() 、
、![]() 满足约束条件
满足约束条件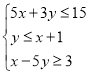 ,若目标函数
,若目标函数![]() (其中
(其中![]() )仅在
)仅在![]() 处取得最大值,则
处取得最大值,则![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】
作出不等式组对应的平面区域,比较直线![]() 与直线
与直线![]() 的斜率的大小关系,利用
的斜率的大小关系,利用![]() 的几何意义,即可得到结论.
的几何意义,即可得到结论.
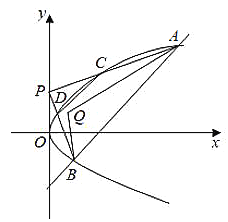
作出不等式组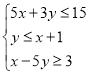 所表示的可行域如下图所示:
所表示的可行域如下图所示:
化目标函数为直线的斜截式得![]() ,则
,则![]() 为直线
为直线![]() 在
在![]() 轴上的截距,
轴上的截距,
![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() .
.
直线![]() 的斜率为
的斜率为![]() ,下面讨论直线
,下面讨论直线![]() 与直线
与直线![]() 斜率的大小.
斜率的大小.
①当![]() 时,即
时,即![]() 时,平移直线
时,平移直线![]() ,可知当该直线经过可行域顶点
,可知当该直线经过可行域顶点![]() 时,该直线在
时,该直线在![]() 轴上的截距最大,此时
轴上的截距最大,此时![]() 取最大值,合乎题意;
取最大值,合乎题意;
②当![]() 时,即当
时,即当![]() 时,平移直线
时,平移直线![]() ,可知当该直线与直线
,可知当该直线与直线![]() 重合时,该直线在
重合时,该直线在![]() 轴上的截距最大,此时
轴上的截距最大,此时![]() 取最大值,不合乎题意;
取最大值,不合乎题意;
③当![]() 时,即当
时,即当![]() 时,平移直线
时,平移直线![]() ,可知当该直线经过可行域的顶点
,可知当该直线经过可行域的顶点![]() 时,该直线在
时,该直线在![]() 轴上的截距最大,此时
轴上的截距最大,此时![]() 取最大值,不合乎题意.
取最大值,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
故答案为:![]() .
.


练习册系列答案
相关题目
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
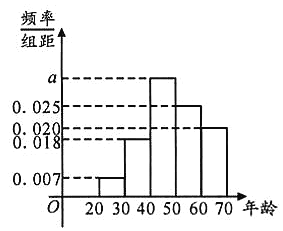
、![]() 分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
年龄(单位:岁) |
|
|
|
|
|
保费(单位:元) |
|
|
|
|
|
(1)求频率分布直方图中实数![]() 的值,并求出该样本年龄的中位数;
的值,并求出该样本年龄的中位数;
(2)现分别在年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中各选出
中各选出![]() 人共
人共![]() 人进行回访.若从这
人进行回访.若从这![]() 人中随机选出
人中随机选出![]() 人,求这
人,求这![]() 人所交保费之和大于
人所交保费之和大于![]() 元的概率.
元的概率.