Question

15．已知曲线C₁：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），过点P（-1，1）的直线l上的动点Q到原点的最短距离为$\sqrt{2}$
（1）求直线l的方程；
（2）若曲线C₁和直线l交于M，N两点，且以MN为直径的圆过坐标原点O，当S_△OMN=$\frac{2\sqrt{10}}{3}$时，求曲线C₁的方程．

Answer 1

分析 （1）通过设直线l的方程为y-1=k[（x-（-1）]，利用原点到该直线的距离为$\sqrt{2}$，计算即得结论；
（2）通过∠MON=$\frac{π}{2}$及三角形面积公式可知MN=$\frac{4\sqrt{5}}{3}$，利用两点间距离公式及直角三角形中斜边中线等于斜边一半构造方程组，进而计算可得结论．

解答 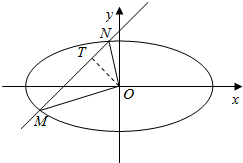解：（1）根据已知条件，设直线l的方程为y-1=k[（x-（-1）]，
化简得kx-y+k+1=0，
依题意，得d=$\frac{|k+1|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$，
解得：k=1，
∴直线l的方程为：x-y+2=0；
（2）依题意，∠MON=$\frac{π}{2}$，
则S_△OMN=$\frac{2\sqrt{10}}{3}$=$\frac{\sqrt{2}}{2}$MN，即MN=$\frac{4\sqrt{5}}{3}$，
联立直线l与椭圆方程，消去y可知：（a²+b²）x²+4a²x+a²（4-b²）=0，
由韦达定理可知：x_M+x_N=-$\frac{4{a}^{2}}{{a}^{2}+{b}^{2}}$，x_Mx_N=$\frac{{a}^{2}（4-{b}^{2}）}{{a}^{2}+{b}^{2}}$，
一方面，MN=$\frac{4\sqrt{5}}{3}$=$\sqrt{（{x}_{M}-{x}_{N}）^{2}+（{y}_{M}-{y}_{N}）^{2}}$=$\sqrt{2}$•$\sqrt{（{x}_{M}+{x}_{N}）^{2}-4{x}_{M}{x}_{N}}$=$\frac{2\sqrt{2}ab}{{a}^{2}+{b}^{2}}$•$\sqrt{{a}^{2}+{b}^{2}-4}$，
整理得：10（a²+b²）²=9a²b²（a²+b²-4），①
另一方面，$\frac{1}{2}$MN=$\sqrt{（\frac{{x}_{M}{+x}_{N}}{2}）^{2}+（\frac{{y}_{M}+{y}_{N}}{2}）^{2}}$，
即$\frac{2\sqrt{5}}{3}$=$\sqrt{\frac{4{a}^{4}}{（{a}^{2}+{b}^{2}）^{2}}+（-\frac{2{a}^{2}}{{a}^{2}+{b}^{2}}+2）^{2}}$，
整理得：a²b²=2（a²-b²）²、9a²b²=2（a²+b²）²，②
联立①、②，解得：a²=6、b²=3，
于是曲线C₁的方程为：$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1$．

点评 本题考查直线与圆锥曲线的关系，考查数形结合能力，注意解题方法的积累，属于中档题．