题目内容
6.已知A(2,-1),B(-1,1),O为坐标原点,A,B,M三点共线,且O$\vec M=\frac{1}{3}$$O\vec A+λO\vec B$,则点M的坐标为(0,$\frac{1}{3}$).分析 由已知A,B,M三点共线,且O$\vec M=\frac{1}{3}$$O\vec A+λO\vec B$,得到λ,然后利用向量相等求坐标.
解答 解:因为A,B,M三点共线,且O$\vec M=\frac{1}{3}$$O\vec A+λO\vec B$,所以$\frac{1}{3}+λ$=1,所以$λ=\frac{2}{3}$,
设M(x,y),则(x,y)=$\frac{1}{3}$(2,-1)+$\frac{2}{3}$(-1,1),所以$\left\{\begin{array}{l}{x=0}\\{y=\frac{1}{3}}\end{array}\right.$,故M$({0,\frac{1}{3}})$;
故答案为:(0,$\frac{1}{3}$).
点评 本题考查了平面向量共线的性质以及向量相等确定坐标,属于基础题,

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.已知直线l1经过A(-1,4),B(-6,-1)两点,直线l2倾斜角为135°,那么l1与l2( )
| A. | 平行 | B. | 垂直 | C. | 重合 | D. | 相交但不垂直 |
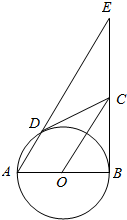 如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.
如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC. 如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$.CF与平面 ABCD垂直,CF=2.求二面角B-AF-D的大小.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$.CF与平面 ABCD垂直,CF=2.求二面角B-AF-D的大小.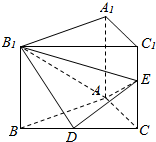 如图,在直三棱柱ABC-A1B1C1中,D,E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.