题目内容
【题目】为响应党的号召,坚决打赢脱贫攻坚战,某地区实行了帮扶单位定点帮扶扶贫村脱贫.为了解该地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:
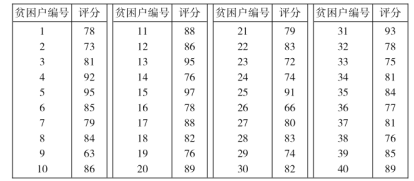
现按贫困户编号从小到大的顺序分组,用系统抽样法从40名贫困户中抽取容量为10的样本.
(1)若在第一分段里随机抽到的第一个样本的评分数据为81,记第二和第十个样本的评分数据分别为a,b,请写出a,b的值;
(2)若10个样本的评分数据分别为92,84,86,78,89,74,83,78,77,89.请你计算所抽到的10个样本的平均数![]() 和方差
和方差![]() ;
;
(3)在(1)条件下,若贫困户的满意度评分在![]() 之间,则满意度等级为“A级”.试应用样本估计总体的思想,用(2)中的样本数据,估计在满意度为“A级”的贫困户中随机地抽取2户,所抽到2户的满意度评分均“超过80”的概率.
之间,则满意度等级为“A级”.试应用样本估计总体的思想,用(2)中的样本数据,估计在满意度为“A级”的贫困户中随机地抽取2户,所抽到2户的满意度评分均“超过80”的概率.
(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() ,
,![]() ;(2)83;33;(3)0.3
;(2)83;33;(3)0.3
【解析】
(1)根据系统抽样的规则,第一组编号为3,则随后k组的编号为![]() ,即可确定系统抽样抽取的样本编号,可得a,b的值;
,即可确定系统抽样抽取的样本编号,可得a,b的值;
(2)利用平均数![]() 和方差
和方差![]() 的计算公式进行计算可得答案;
的计算公式进行计算可得答案;
(3)先确定满意度为“A级”的贫困户的人数,从中随机抽取2户,共有几种可能,算得满意度均超过“80分”的个数,利用古典概型计算可得答案.
解:(1)![]() ,
,![]()
(2)![]()
![]()
![]()
(3)在(2)的条件下![]()
所以评分在![]() .即满意度为“A级”的贫困户有84,86,78,84,78
.即满意度为“A级”的贫困户有84,86,78,84,78
从中随机抽取2户,共有以下10种可能
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
所以可算得满意度均超过“80分”的概率为![]()
所以可以估计在满意度为“A级”的贫困户中随机抽取两户,打分均超过“80”分的概率约为0.3.

【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()