题目内容
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
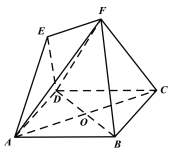
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取AO中点H,连结EH,则EH⊥BD,又AC⊥BD,由此可证;
(Ⅱ)以H为原点,HA为x轴,在平面ABCD中过H作AC的垂线为y轴,HE为z轴,建立空间直角坐标系,由(Ⅰ)知,∠EAH为AE与平面ABCD所成的角,再根据平面的法向量的夹角即可求出答案.
(Ⅰ)证:取AO中点H,连结EH,则EH⊥平面ABCD,
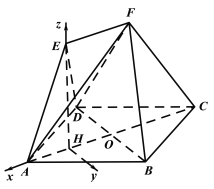
∵BD在平面ABCD内,∴EH⊥BD,
又菱形ABCD中,AC⊥BD,且EH∩AC=H,
EH,AC在平面EACF内,
∴BD⊥平面EACF,
∴BD⊥平面ACF;
(Ⅱ)解:由(Ⅰ)知EH⊥平面ABCD,
∴以H为原点,HA为x轴,在平面ABCD中过H作AC的垂线为y轴,HE为z轴,建立空间直角坐标系,
∵EH⊥平面ABCD,∴∠EAH为AE与平面ABCD所成的角,即∠EAH=45°,
∵AB=4,∴AO=2![]() ,AH
,AH![]() ,EH
,EH![]() ,
,
∴H(0,0,0),A(![]() ,0,0),D(
,0,0),D(![]() ,﹣2,0),O(
,﹣2,0),O(![]() ,0,0),E(0,0,
,0,0),E(0,0,![]() ),
),
平面ABCD的法向量![]() (0,0,1),
(0,0,1),
![]() (﹣2
(﹣2![]() ,0,0),
,0,0),![]() (
(![]() ),
),
∵EF![]() AC,∴
AC,∴![]() (﹣2
(﹣2![]() λ,0,0),
λ,0,0),
设平面DEF的法向量![]() (x,y,z),
(x,y,z),
则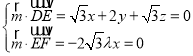 ,取y
,取y![]() ,得
,得![]() (0,
(0,![]() ,﹣2),
,﹣2),
∴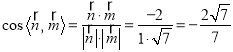 ,
,
∴平面DEF与平面ABCD所成角的正弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.
【题目】今年情况特殊,小王在居家自我隔离时对周边的水产养殖产业进行了研究.![]() 、
、![]() 两个投资项目的利润率分别为投资变量
两个投资项目的利润率分别为投资变量![]() 和
和![]() .根据市场分析,
.根据市场分析,![]() 和
和![]() 的分布列分别为:
的分布列分别为:
| 5% | 10% | ||
| 0.8 | 0.2 | ||
| 2% | 8% | 12% | |
| 0.2 | 0.5 | 0.3 | |
(1)若在![]() 两个项目上各投资
两个项目上各投资![]() 万元,
万元,![]() 和
和![]() 分别表示投资项目
分别表示投资项目![]() 和
和![]() 所获得的利润,求方差
所获得的利润,求方差![]() ,
,![]() ;
;
(2)若在![]() 两个项目上共投资
两个项目上共投资![]() 万元,那么如何分配,能使投资
万元,那么如何分配,能使投资![]() 项目所得利润的方差与投资
项目所得利润的方差与投资![]() 项目所得利润的方差的和最小,最小值是多少?
项目所得利润的方差的和最小,最小值是多少?
(注:![]() )
)