题目内容
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.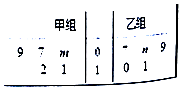
(1)分别求出m,n的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差s甲2和s乙2 , 并由此分析两组技工的加工水平.
【答案】
(1)解:∵两组技工在单位时间内加工的合格零件平均数都为9.
∴由茎叶图得: 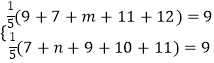 ,
,
解得m=6,n=8.
(2)解: ![]() =
= ![]() [(6﹣9)2+(7﹣9)2+(9﹣9)2+(11﹣9)2+(12﹣9)2]=
[(6﹣9)2+(7﹣9)2+(9﹣9)2+(11﹣9)2+(12﹣9)2]= ![]() .
.
![]() =
= ![]() [(7﹣9)2+(8﹣9)2+(9﹣9)2+(10﹣9)2+(11﹣9)2]=2.
[(7﹣9)2+(8﹣9)2+(9﹣9)2+(10﹣9)2+(11﹣9)2]=2.
∵两组技工在单位时间内加工的合格零件平均数都为9, ![]() <
< ![]() ,
,
∴两组技工平均数相等,但乙组技工较稳定,故乙组技工加工水平高.
【解析】(1)根据茎叶图得到在单位时间内每个技工加工的合格零件数,根据平均数列出等式,分别计算出m,n,(2)根据方差公式求出甲,乙两组技工在单位时间内加工的合格零件的方差,由于S 乙 2 < S 甲 2,可得出 乙组技工加工水平高.
【考点精析】通过灵活运用茎叶图和极差、方差与标准差,掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少;标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差即可以解答此题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目