题目内容
【题目】已知△ABC的周长为 
+1，且sinA+sinB= sinC
（I）求边AB的长；
（Ⅱ）若△ABC的面积为 
sinC，求角C的度数．
【答案】解：（I）由题意及正弦定理，得AB+BC+AC= 
+1．BC+AC= AB， 两式相减，得：AB=1．
（Ⅱ）由△ABC的面积= 
BCACsinC= 
sinC，得
BCAC= 
，
∴AC2+BC2=（AC+BC）2﹣2ACBC=2﹣ 
= 
，
由余弦定理，得 
，
所以C=60°．
【解析】（I）先由正弦定理把sinA+sinB= 
sinC转化成边的关系，进而根据三角形的周长两式相减即可求得AB．（2）由△ABC的面积根据面积公式求得BCAC的值，进而求得AC2+BC2 ， 代入余弦定理即可求得cosC的值，进而求得C．
练习册系列答案
相关题目
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x（0＜x≤10）与销售价格y（单位：万元/辆）进行整理，得到如表的对应数据：
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
（1）试求y关于x的回归直线方程；（参考公式： 
= 
， 
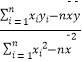=y﹣ 
）
（2）已知每辆该型号汽车的收购价格为w=0.01x3﹣0.09x2﹣1.45x+17.2万元，根据（1）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润L（x）最大？（利润=售价﹣收购价）
