题目内容
【题目】如图,正方体ABCD-A1B1C1D1的棱长为a , M为BD1的中点,N在A1C1上,且满足|A1N|=3|NC1|.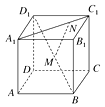
(1)求MN的长;
(2)试判断△MNC的形状.
【答案】
(1)解:以D为原点,建立空间直角坐标系,
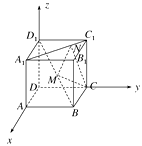
并设正方体边长为a,则B(a,a,0),D1(0,0,a),A1(a,0,a),C1(0,a,a),C(0,a,0),M( ![]() a,
a, ![]() a,
a, ![]() a),N(
a),N( ![]() a,
a, ![]() a,a),
a,a),
∴|MN|= ![]() =
= ![]() a.
a.
(2)解:∵ ![]() =(-
=(- ![]() a,
a, ![]() a,
a, ![]() a),
a), ![]() =(-
=(- ![]() a,
a, ![]() a,-
a,- ![]() a),
a), ![]() =(-
=(- ![]() a,
a, ![]() a,-a),
a,-a),
∴ ![]() ·
· ![]() =
= ![]() a2+
a2+ ![]() a2-
a2- ![]() a2=0,∴MN⊥MC,∴△MNC是直角三角形.
a2=0,∴MN⊥MC,∴△MNC是直角三角形.
【解析】本题根据题意可以选用坐标法来解题,根据向量的相关知识及空间线段长计算公式:![]() 及两向量数量积等于零得到两向量垂直,解出本题。
及两向量数量积等于零得到两向量垂直,解出本题。
【考点精析】关于本题考查的棱柱的结构特征,需要了解两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形才能得出正确答案.

练习册系列答案
相关题目