题目内容
【题目】(本小题满分12分)
在如图所示的多面体中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1) 解法1
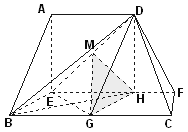
证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() . …………2分
. …………2分
过![]() 作
作![]() 交
交![]() 于
于![]() ,则
,则![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() . …………4分
. …………4分
∵![]() ,∴四边形
,∴四边形![]() 平行四边形,
平行四边形,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴四边形![]() 为正方形,
为正方形,
∴![]() , ……………6分
, ……………6分
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ⊥平面
⊥平面![]() . ………………………7分
. ………………………7分
∵![]() 平面
平面![]() ,
,
∴![]() . ………………………8分
. ………………………8分
(2)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴平面![]() ⊥平面
⊥平面![]()
由(1)可知![]()
∴![]() ⊥平面
⊥平面![]()
∵![]() 平面
平面![]()
∴![]() ……………………9分
……………………9分
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]()
∵四边形![]() 是正方形,
是正方形,
∴![]()
∵![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() ⊥平面
⊥平面![]()
∴![]() ⊥
⊥![]() Z|X|X|K]
Z|X|X|K]
∴![]() 是二面角
是二面角![]() 的平面角, ………………………12分
的平面角, ………………………12分
由计算得![]()
∴![]() ………………………13分
………………………13分
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .………………………14分
.………………………14分
解法2
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,
,
又![]() ,
,
∴![]() 两两垂直. ……………………2分
两两垂直. ……………………2分
以点E为坐标原点,![]() 分别为
分别为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
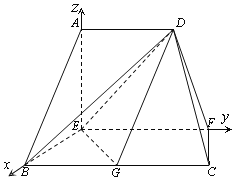
由已知得,![]() (0,0,2),
(0,0,2),![]() (2,0,0),
(2,0,0),
![]() (2,4,0),
(2,4,0),![]() (0,3,0),
(0,3,0),![]() (0,2,2),
(0,2,2),
![]() (2,2,0). …………………………4分
(2,2,0). …………………………4分
∴![]() ,
,![]() ,………6分
,………6分
∴![]() , ………7分
, ………7分
∴![]() . …………………………8分
. …………………………8分
(2)由已知得![]() 是平面
是平面![]() 的法向量. ………………………9分
的法向量. ………………………9分
设平面![]() 的法向量为
的法向量为![]() ,
,
∵![]() ,
,
∴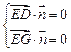 ,即
,即![]() ,令
,令![]() ,得
,得![]() . ……………12分
. ……………12分
设平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,
,
则![]() …………………………13分
…………………………13分
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() . …………………………14分
. …………………………14分
【解析】
(1)证明EB,EF,EA两两垂直,以点E为坐标原点,EB,EF,EA分别为x,y,z轴,建立空间直角坐标系用坐标表示点与向量,证明
![]() ,可得BD⊥EG;
,可得BD⊥EG;
(2)由已知得![]() 是平面DEF的法向量,求出平面DEG的法向量
是平面DEF的法向量,求出平面DEG的法向量
![]() ,利用向量的夹角公式,可求平面DEG与平面DEF所成锐二面角的余弦值.
,利用向量的夹角公式,可求平面DEG与平面DEF所成锐二面角的余弦值.
(Ⅰ)![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .又
.又![]() ,
,
![]() BE,EF,AE两两垂直.
BE,EF,AE两两垂直.
以点E为坐标原点,EB,EF,EA分别为x,y,z轴,
建立空间直角坐标系,
由已知得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() .
.
(Ⅱ)由已知得![]() 是平面DEF的法向量,
是平面DEF的法向量,
设平面的DEG法向量为![]() ,
,
![]() ,
,![]() ,
,
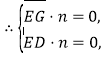 即
即![]() 令
令![]() ,得
,得![]() ,
,
设平面DEG与平面DEF所成锐二面角的大小为θ,
则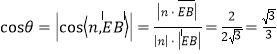 .
.
![]() 平面DEG与平面DEF所成锐二面角的余弦值为
平面DEG与平面DEF所成锐二面角的余弦值为![]() .
.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司底薪70元,每单抽成2元;乙公司无底薪,40单以内(含40单)的部分每单抽成4元,超出40单的部分每单抽成6元.假设同一公司的送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到如下频数表:
甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
(1)现从甲公司记录的这100天中随机抽取两天,求这两天送餐单数都大于40的概率;
(2)若将频率视为概率,回答以下问题:
(i)记乙公司送餐员日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
