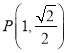题目内容
【题目】已知在平面直角坐标系中,直线l过点P(1,2).
(1)若直线l在x轴和y轴上的截距相等,求直线l的方程;
(2)求坐标原点O到直线l距离取最大值时的直线l的方程;
(3)设直线l与x轴正半轴、y轴正半轴分别相交于A,B两点,当|PA||PB|最小时,求直线l的方程.
【答案】(1)y=2x,x+y=3(2)x+2y-5=0(3)x+y-3=0
【解析】
(1)直线l经过原点时满足条件,可得方程为:y=2x.直线l不经过原点时,设方程为:x+y=a,把点P的坐标代入即可得出a.
(2)坐标原点O到直线l距离取最大值时,直线l⊥OP.可得:kOP=2,kl![]() .利用点斜式即可得出.
.利用点斜式即可得出.
(3)设直线l的方程为:y﹣2=k(x﹣1),k<0.可得A(1![]() ,0),B(0,2﹣k).利用两点之间的距离公式可得|PA||PB|,再利用基本不等式的性质即可得出.
,0),B(0,2﹣k).利用两点之间的距离公式可得|PA||PB|,再利用基本不等式的性质即可得出.
(1)直线l经过原点时满足条件,可得方程为:y=2x.
直线l不经过原点时,设方程为:x+y=a,可得:a=1+2=3.
可得方程为:x+y=3.
综上可得:直线l的方程为:y=2x,x+y=3.
(2)坐标原点O到直线l距离取最大值时,直线l⊥OP.
可得:kOP=2,∴kl![]() .
.
∴坐标原点O到直线l距离取最大值时的直线l的方程为:y﹣2![]() (x﹣1),化为:x+2y﹣5=0.
(x﹣1),化为:x+2y﹣5=0.
(3)设直线l的方程为:y﹣2=k(x﹣1),k<0.
可得A(1![]() ,0),B(0,2﹣k).
,0),B(0,2﹣k).
|PA||PB|![]()
![]() 4,
4,
当且仅当k=﹣1时取等号.
此时直线l的方程为:y﹣2=﹣(x﹣1),化为:x+y﹣3=0.

练习册系列答案
相关题目