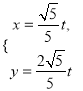题目内容
【题目】有下列命题：①边长为1的正四面体的内切球半径为
；
②正方体的内切球、棱切球（正方体的每条棱都与球相切）、外接球的半径之比为1：
；
③棱长为1的正方体ABCD-A1B1C1D1的内切球被平面A1BD截得的截面面积为
．
其中正确命题的序号是______（请填所有正确命题的序号）；
【答案】①②③
【解析】
运用正四面体的性质和体积公式，结合等积法可得球的半径，可判断①；
由正方体与内切球、棱切球和外接球的关系，求得半径，可判断②；
求得正方体内切球半径，结合球的截面性质，以及勾股定理和等边三角形的性质，即可判断③．
①边长为1的正四面体的高为h
，
可得正四面体的体积为V
h
，
设内切球的半径为r，由等积法可得VrSr4，（S为正四面体的全面积）
解得r
，故①正确；
②设边长为1的正方体的内切球、棱切球（正方体的每条棱都与球相切）、外接球的半径
分别为r1，r2，r3，可得2r1＝1，2r2
，2r3
，
即有r1：r2：r3＝1：
，故②正确；
③棱长为1的正方体ABCD﹣A1B1C1D1的内切球的半径为
，
设内心为I，可得A1I
，I在截面的射影为等边三角形A1BD的中心O，
可得OI
，
由球的截面的性质可得截面圆的半径为
，可得截面圆的面积为
，故③正确．
故答案为：①②③．
练习册系列答案
相关题目
