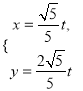题目内容
【题目】若对于曲线![]() 上任意点处的切线
上任意点处的切线![]() ,总存在
,总存在![]() 上处的切线
上处的切线![]() ,使得
,使得![]() ,则实数
,则实数![]() 的取值范围是__________.
的取值范围是__________.
【答案】![]()
【解析】f(x)=﹣ex﹣x的导数为f′(x)=﹣ex﹣1,
设(x1,y1)为f(x)上的任一点,
则过(x1,y1)处的切线l1的斜率为k1=﹣ex1﹣1,
g(x)=2ax+sinx的导数为g′(x)=2a+cosx,
过g(x)图象上一点(x2,y2)处的切线l2的斜率为k2=2a+cosx2.
由l1⊥l2,可得(﹣ex1﹣1)(2a+cosx2)=﹣1,
即2a+cosx2=![]() ,
,
任意的x1∈R,总存在x2∈R使等式成立.
则有y1=2a+cosx2的值域为A=[2a﹣1,2a+1].
y2=![]() 的值域为B=(0,1),
的值域为B=(0,1),
有BA,即(0,1)[2a﹣1,2a+1].
即![]() ,
,
解得0≤a≤![]() .
.
故答案为:[0, ![]() ].
].

练习册系列答案
相关题目