题目内容
【题目】已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1 , l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
【答案】
(1)
证明:连接RF,PF,
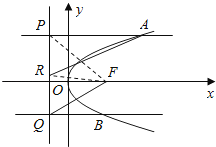
由AP=AF,BQ=BF及AP∥BQ,得∠AFP+∠BFQ=180°,
∴∠PFQ=90°,
∵R是PQ的中点,
∴RF=RP=RQ,
∴△PAR≌△FAR,
∴∠PAR=∠FAR,∠PRA=∠FRA,
∵∠BQF+∠BFQ=180°﹣∠QBF=∠PAF=2∠PAR,
∴∠FQB=∠PAR,
∴∠PRA=∠PRF,
∴AR∥FQ
(2)
A(x1,y1),B(x2,y2),
F( ![]() ,0),准线为 x=﹣
,0),准线为 x=﹣ ![]() ,
,
S△PQF= ![]() |PQ|=
|PQ|= ![]() |y1﹣y2|,
|y1﹣y2|,
设直线AB与x轴交点为N,
∴S△ABF= ![]() |FN||y1﹣y2|,
|FN||y1﹣y2|,
∵△PQF的面积是△ABF的面积的两倍,
∴2|FN|=1,∴xN=1,即N(1,0).
设AB中点为M(x,y),由 ![]() 得
得 ![]() =2(x1﹣x2),
=2(x1﹣x2),
又 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即y2=x﹣1.
,即y2=x﹣1.
∴AB中点轨迹方程为y2=x﹣1.
【解析】(1)连接RF,PF,利用等角的余角相等,证明∠PRA=∠PRF,即可证明AR∥FQ;(2)利用△PQF的面积是△ABF的面积的两倍,求出N的坐标,利用点差法求AB中点的轨迹方程.本题考查抛物线的方程与性质,考查轨迹方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目

