题目内容
4.反证法证明的关键是在正确的假设下得出矛盾,这个矛盾可以是( )①与已知矛盾;②与假设矛盾;③与定义、定理、公理、法则矛盾;④与事实矛盾.
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②③④ |
分析 直接利用反证法的定义判断正误即可.
解答 解:利用已知定义、定理、公理等基本原理逐步推证出一个与命题的条件或已证明的定理或公认的简单事实相矛盾的结论,以此说明原假设的结论不成立,从而肯定原命题的结论成立的方法称为反证法.
①与已知条件矛盾;正确.
②与假设矛盾;正确.
③与定义、定理、公理、法则矛盾;正确.
④与事实矛盾.正确.
故选:D.
点评 本题考查反证法定义的连结与应用,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若tanα=3,则$\frac{2sinαcosα}{si{n}^{2}α+2co{s}^{2}α}$的值为( )
| A. | $\frac{6}{11}$ | B. | $\frac{3}{11}$ | C. | $\frac{11}{3}$ | D. | $\frac{11}{6}$ |
9.已知实数ai,bi∈R,(i=1,2,…n),且满足a12+a22+…an2=1,b12+b22+…bn2=1,则a1b1+a2b2+…+anbn的最大值为( )
| A. | 1 | B. | 2 | C. | n$\sqrt{2}$ | D. | 2$\sqrt{n}$ |
13.已知函数f(x)=$\left\{\begin{array}{l}\frac{2}{x},x≥2\\{(x-1)^3},0<x<2\end{array}\right.$若关于x的方程f(x)=kx有两个不同的实根,则实数k的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (0,1) | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
14.若角α和角β的终边关于x轴对称,则角α可以用角β表示为( )
| A. | 2kπ+β (k∈Z) | B. | 2kπ-β (k∈Z) | C. | kπ+β (k∈Z) | D. | kπ-β (k∈Z) |
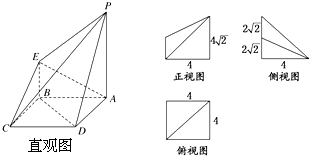 如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).