题目内容
19. 如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).(1)求四棱锥P-ABCD的体积;
(2)求证:BD∥平面PEC;
(3)求证:AE⊥平面PBC.
分析 (1)结合三视图,得到几何体的相关棱长,求四棱锥P-ABCD的底面面积和高,然后求出体积;
(2)连接AC交BD于O点,取PC中点F,连接OF,要证明BD∥平面PEC,只需证明BD平行平面PEC内的直线EF即可;
(3)要证AE⊥平面PBG,只需证明PB⊥AE,BC⊥AE即可得证.
解答 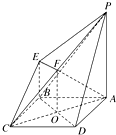 (本题满分14分)
(本题满分14分)
解:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,
且PA=4$\sqrt{2}$,BE=2$\sqrt{2}$,AB=AD=CD=CB=4,
∴VP-ABCD=$\frac{1}{3}$PA×SABCD=$\frac{1}{3}$×4$\sqrt{2}$×4×4=$\frac{64\sqrt{2}}{3}$.…(4分)
(2)证明:连结AC交BD于O点,取PC中点F,连结OF,
∵EB∥PA,且EB=$\frac{1}{2}$PA,又OF∥PA,且OF=$\frac{1}{2}$PA,
∴EB∥OF,且EB=OF,
∴四边形EBOF为平行四边形,
∴EF∥BD.又EF?平面PEC,BD?平面PEC,所以BD∥平面PEC.…(9分)
(3)∵$\frac{EB}{AB}=\frac{BA}{PA}=\frac{1}{\sqrt{2}}$,∠EBA=∠BAP=90°,
∴△EBA∽△BAP,
∴∠PBA=∠BEA,∴∠PBA+∠BAE=∠BEA+∠BAE=90°,
∴PB⊥AE.
又∵BC⊥平面APEB,
∴BC⊥AE,
∴AE⊥平面PBG,…(14分)
点评 本题考查三视图,几何体的条件,直线与平面垂直和平行的判定,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若集合A={2,4},B={1,m2},则“A∩B={4}”是“m=2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.在△ABC中,cosB=-$\frac{5}{13}$,cosC=$\frac{4}{5}$,tanA的值为( )
| A. | $\frac{33}{16}$ | B. | -$\frac{33}{56}$ | C. | $\frac{33}{56}$ | D. | $\frac{63}{16}$ |
4.反证法证明的关键是在正确的假设下得出矛盾,这个矛盾可以是( )
①与已知矛盾;②与假设矛盾;③与定义、定理、公理、法则矛盾;④与事实矛盾.
①与已知矛盾;②与假设矛盾;③与定义、定理、公理、法则矛盾;④与事实矛盾.
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②③④ |
9. 如图是导函数y=f′(x)的图象,则函数f(x)在开区间(a,b)内有极小值点( )个;哪个区间是减函数( )
如图是导函数y=f′(x)的图象,则函数f(x)在开区间(a,b)内有极小值点( )个;哪个区间是减函数( )
 如图是导函数y=f′(x)的图象,则函数f(x)在开区间(a,b)内有极小值点( )个;哪个区间是减函数( )
如图是导函数y=f′(x)的图象,则函数f(x)在开区间(a,b)内有极小值点( )个;哪个区间是减函数( )| A. | 1;(x1,x3) | B. | 1;(x2,x4) | C. | 2;(x4,x6) | D. | 2;(x5,x6) |