题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}\frac{2}{x},x≥2\\{(x-1)^3},0<x<2\end{array}\right.$若关于x的方程f(x)=kx有两个不同的实根,则实数k的取值范围是( )| A. | (0,$\frac{1}{2}$) | B. | (0,1) | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
分析 首先画出函数图象,利用数形结合和函数的单调性即可得出.
解答 解:如图所示: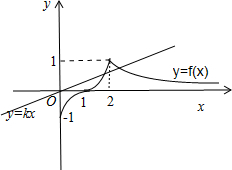
①当x≥2时,由函数f(x)=$\frac{2}{x}$单调递减,可得:0<f(x)=$\frac{2}{x}$;
②当0<x<2时,由函数f(x)=(x-1)3单调递增可得:-1<f(x)<1.
由图象可知:由0<2k<1可得0<k<$\frac{1}{2}$,
故当0<k<$\frac{1}{2}$时,函数y=kx与y=f(x)的图象有且只有两个交点,
∴满足关于x的方程f(x)=kx有两个不同的实根的实数k的取值范围是
(0,$\frac{1}{2}$).
故选:A.
点评 本题考查了利用数形结合求方程根的问题;熟练掌握数形结合的思想方法和函数的单调性是解题的关键.

练习册系列答案
相关题目
3.已知函数$y=\sqrt{x-1}+{log_3}(3-x)$,则其定义域为( )
| A. | [1,3) | B. | (-∞,1]∪(3,+∞) | C. | (1,3] | D. | (-∞,1)∪[3,+∞) |
4.反证法证明的关键是在正确的假设下得出矛盾,这个矛盾可以是( )
①与已知矛盾;②与假设矛盾;③与定义、定理、公理、法则矛盾;④与事实矛盾.
①与已知矛盾;②与假设矛盾;③与定义、定理、公理、法则矛盾;④与事实矛盾.
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②③④ |
18.已知等差数列{an}满足${a}_{3}^{2}$+${a}_{8}^{2}$+2a3a8=9,则其前10项和( )
| A. | 15 | B. | 12 | C. | ±12 | D. | ±15 |
5.等比数列{an}中,a1=$\frac{1}{8}$,q=2,则a6等于是( )
| A. | ±4 | B. | 4 | C. | ±$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
2.若sin2α=$\frac{1}{4}$,$\frac{π}{4}$<α<$\frac{π}{2}$,则cosα-sinα的值( )
| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |