题目内容
2．甲、乙、丙、丁四人参加某运动会射击项目选拔赛，四人的平均成绩和方差如下表所示：| 甲 | 乙 | 丙 | 丁 | |
| 平均环数x | 8.3 | 8.8 | 8.8 | 8.7 |
| 方差s2 | 3.5 | 3.6 | 2.2 | 5.4 |
分析 根据平均数表示成绩的高低，方差表示成绩的稳定性，进行比较即可得出结论．
解答 解：∵甲、乙、丙、丁四人的平均环数乙和丙均为8.8环，最大，
甲、乙、丙、丁四人的射击环数的方差中丙最小，
∴丙的射击水平最高且成绩最稳定，
∴从这四个人中选择一人参加该运动会射击项目比赛，
最佳人选是丙．
故答案为：丙．
点评 本题考查了利用平均数与方差表示一组数据的数字特征的应用问题，是基础题目．
练习册系列答案
相关题目
7．如图，四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{DC}$，则必有（ ）
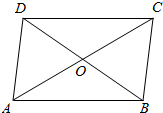
| A． | $\overrightarrow{AD}$=$\overrightarrow{CB}$ | B． | $\overrightarrow{OA}$=$\overrightarrow{OC}$ | C． | $\overrightarrow{AC}$=$\overrightarrow{DB}$ | D． | $\overrightarrow{DO}$=$\overrightarrow{OB}$ |