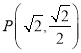题目内容
【题目】设函数![]() .
.
(1)若不等式![]() 对任意的
对任意的![]() ,
,![]() 都成立,求实数m的取值范围;
都成立,求实数m的取值范围;
(2)关于x的方程![]() 在
在![]() 上有且只有一个解,求实数k的取值范围.
上有且只有一个解,求实数k的取值范围.
参考数据:![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
![]() 由题意,将
由题意,将![]() 转化为
转化为![]() ,进而转化为
,进而转化为![]() ,求出
,求出![]() 单调性得出最值即可求出m取值取值范围;
单调性得出最值即可求出m取值取值范围;![]() 将方程
将方程![]() 在
在![]() 上有且只有一个解,转化为
上有且只有一个解,转化为![]() ,
,
令![]() ,研究其单调性和最值即可得到实数k的取值范围.
,研究其单调性和最值即可得到实数k的取值范围.
(1)由题![]() ,即
,即![]() 对任意的
对任意的![]() 都成立,
都成立,
令![]() ,则
,则![]() 为关于k的一次函数,
为关于k的一次函数,![]() .
.
因为![]() ,
,![]()
令![]() ,
,![]() ,因为
,因为![]() ,
,
![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
所以![]() ,即m的取值范围是
,即m的取值范围是![]() .
.
(2)方程![]() 在
在![]() 上有且只有一个解,
上有且只有一个解,
即关于x的方程![]() 在
在![]() 上有且只有一个解.
上有且只有一个解.
整理方程得![]() ,
,
令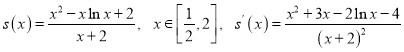 ,
,
令![]() ,则
,则![]()
于是![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,从而
,从而![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,从而
,从而![]() ,
,![]() 单调递增.
单调递增.
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以实数k的取值范围是![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
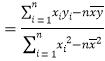 ,
,![]()