题目内容
【题目】设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.,求ξ分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若![]() ,求a:b:c.
,求a:b:c.
【答案】(1)
ξ | 2 | 3 | 4 | 5 | 6 |
P |
|
|
|
|
|
(2)3:2:1
【解析】
试题(1)由已知,分别计算![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 时的概率,得到
时的概率,得到![]() 的分布列.
的分布列.
(2)首先计算![]() 的分布列,进一步计算期望、方差,建立
的分布列,进一步计算期望、方差,建立![]() 的关系式.
的关系式.
试题解析:(1)由已知得到:当两次摸到的球分别是红红时![]() ,此时
,此时![]() ,
,
当两次摸到的球分别是黄黄,红蓝,蓝红时![]() ,此时
,此时![]() ;
;
当两次摸到的球分别是红黄,黄红时![]() ,此时
,此时![]() ;
;
当两次摸到的球分别是黄蓝, 蓝黄时![]() ,此时
,此时![]() ;
;
当两次摸到的球分别是蓝蓝时![]() ,此时
,此时![]() ;
;
所以![]() 的分布列是:
的分布列是:
|
|
|
|
|
|
|
|
|
|
|
|
(2)由已知得到:![]() 有三种取值即
有三种取值即![]() ,所以
,所以![]() 的分布列是:
的分布列是:
|
|
|
|
|
|
|
|
所以: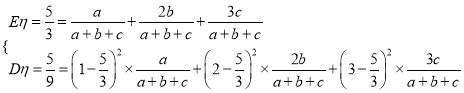
所以![]() .
.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】某家庭为了解冬季用电量![]() (度)与气温
(度)与气温![]() 之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出用电量![]() 关于气温
关于气温![]() 的线性回归方程;
的线性回归方程;
(2)在这5天中随机抽取两天,求至少有一天用电量低于10(度)的概率.
(附:回归直线方程的斜率和截距的最小二乘法估计公式为 ,
,![]() )
)
