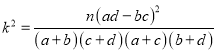题目内容
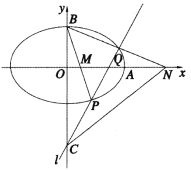
【题目】如图，过抛物线
焦点
的直线与抛物线交于
（其中
点在
轴的上方）两点.
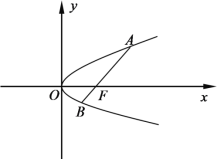
（1）若线段
的长为3，求
到直线
的距离；
（2）证明：
为钝角三角形；
（3）已知
且
，求三角形
的面积
的取值范围.
【答案】（1）
；（2）详见解析；（3）
【解析】
（1）先根据抛物线定义求出
点坐标，再根据点斜式求直线
的方程，最后根据点到直线距离公式求结果；
（2）先设直线方程，与抛物线方程联立，结合韦达定理化简
,根据为负证明结果；
（3）先设直线方程，与抛物线方程联立，结合韦达定理以及面积公式表示三角形
的面积
，再根据对勾函数单调性求值域.
（1）设
，因为
，所以
，
因此
从而
到直线的距离为
；
（2）设直线的方程为
，
由
得
从而
，因此
为钝角三角形；
（3）因为
，所以
，由（2）得
，所以
因为
，所以
，
而
在
上单调递增，所以
【题目】某大学为了解学生对学校食堂服务的满意度，随机调查了50名男生和50名女生，每位学生对食堂的服务给出满意或不满意的评价，得到如图所示的列联表.经计算
的观测值
，则可以推断出（ ）
满意 | 不满意 | |
男 | 30 | 20 |
女 | 40 | 10 |
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
A.该学校男生对食堂服务满意的概率的估计值为
B.调研结果显示，该学校男生比女生对食堂服务更满意
C.有95%的把握认为男、女生对该食堂服务的评价有差异
D.有99%的把握认为男、女生对该食堂服务的评价有差异
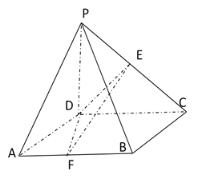
【题目】如图，在三棱锥
中，
，
，O为AC的中点．
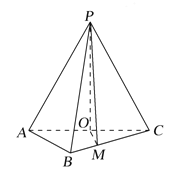
（1）证明：
平面ABC；
（2）若点M在棱BC上，且
，求点C到平面POM的距离．
（3）若点M在棱BC上，且二面角
为30°，求PC与平面PAM所成角的正弦值．
【题目】为迎接2022年北京冬季奥运会，普及冬奥知识，某校开展了“冰雪答题王”冬奥知识竞赛活动．现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生，将他们的比赛成绩（满分为100分）分为6组：
，
，
，
，
，
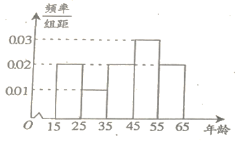
，得到如图所示的频率分布直方图．
（1）求
的值；
（2）估计这100名学生的平均成绩（同一组中的数据用该组区间的中点值为代表）；
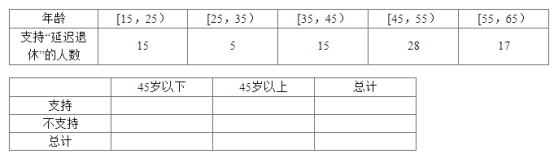
（3）在抽取的100名学生中，规定：比赛成绩不低于80分为“优秀”，比赛成绩低于80分为“非优秀”．请将下面的2×2列联表补充完整，并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”？
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
