Question

【题目】已知椭圆的离心率e满足，右顶点为A，上顶点为B，点C(0，－2)，过点C作一条与y轴不重合的直线l，直线l交椭圆E于P，Q两点，直线BP，BQ分别交x轴于点M，N；当直线l经过点A时，l的斜率为．

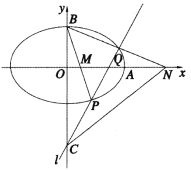
(1)求椭圆E的方程；

(2)证明：为定值．

Answer 1

【答案】（1）（2）证明见解析

【解析】

（1）由得，从而可得，又有，可得，从而可求出椭圆E的方程；

（2）由题知，直线的斜率存在，设直线的方程为

联立直线与椭圆的方程得韦达定理，且=，得，写出直线BP的方程，求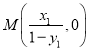得，同理可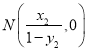得，化简求得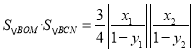=为定值．

解：（1）由解得或（舍去），

∴，又，

，

又，

，，

椭圆E的方程为；

（2）由题知，直线的斜率存在，设直线的方程为，

设，

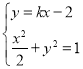由得，

∴，

=

，

∴，

=，

直线BP的方程为，令解得，则，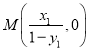

同理可得，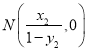

=

==，

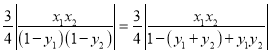
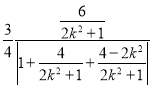为定值．