��Ŀ����
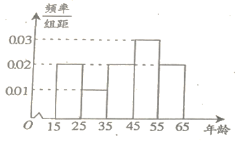
����Ŀ����������Ϊ��Ӧ�����˿����仯����ɵ��Ͷ�����ȱ�����⣬�ⶨ��̨���ӳ�����������������Ϊ���˽����Ƕ����ӳ�����������������̬�ȣ�������粿���е��У����粿������������15��65�����Ⱥ���������100�ˣ��������ݵ�Ƶ�ʷֲ�ֱ��ͼ��֧�����ӳ��������������������ͳ�ƽ�����£�
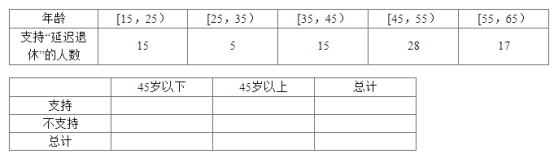
��1��������ͳ��������2��2�����������ж��ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ��45��Ϊ�ֽ��IJ�ͬ��Ⱥ�����ӳ�����������������֧�ֶ��в��죻
��2���ӵ����100����������15��25��25��35���鰴�ֲ�����ķ�����ȡ6�˲μ�ij���ִ���6���������2�ˣ�����2��������1�˵�������25��35֮��ĸ��ʣ�
�ο����ݣ�

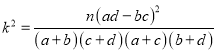 ����n��a+b+c+d
����n��a+b+c+d
���𰸡���1������������2��![]()
��������
(1)�����������ݻ��ܵ����ټ���![]() �жϼ���.
�жϼ���.
(2)���ݷֲ�����Լ�ö�ٷ������ʼ���.
��1����ͳ��������д��2��2���������£�
����45������ | ����45������ | �ܼ� | |
֧�� | 35 | 45 | 80 |
��֧�� | 15 | 5 | 20 |
�ܼ� | 50 | 50 | 100 |
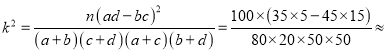 6.25��3.841��
6.25��3.841��
����95%�İ�����Ϊ��45��Ϊ�ֽ���ͬ��Ⱥ�ԡ��ӳ������������ߡ���̬���в��죮���ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ��45��Ϊ�ֽ��IJ�ͬ��Ⱥ�ԡ��ӳ������������ߡ���֧�ֶ��в��죻
��2���ӵ����100����������15��25��25��35���鰴�ֲ�����ķ�����ȡ6�˲μ�ij����
��15��25��25��35���鹲��30�ˣ�
15��25����100��0.02��10��20�ˣ���ȡ20![]() 4�ˣ����ȡ��4��ΪA��B��C��D��
4�ˣ����ȡ��4��ΪA��B��C��D��
25��35����100��0.01��10��10�ˣ���ȡ10![]() 2�ˣ����ȡ��2��Ϊa��b��
2�ˣ����ȡ��2��Ϊa��b��
�ִ���6���������2�˵Ļ����¼�Ϊ��AB��AC��AD��Aa��Ab��BC��BD��Ba��Bb��CD��Ca��Cb��Da��Db��ab��15�������
��2��������1�˵�������25��35֮��ĸ�����![]() ��
��
������2��������1�˵�������25��35֮��ĸ�����![]() ��
��