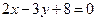题目内容
(本题满分12分)如图所示,F1、F2是双曲线x2 – y2 = 1的两个焦点,O为坐标原点,
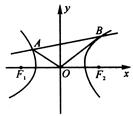
圆O是以F1F2为直径的圆,直线l:y = kx + b与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当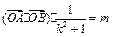 ,且满足2≤m≤4时,
,且满足2≤m≤4时,
求△AOB面积的取值范围.

圆O是以F1F2为直径的圆,直线l:y = kx + b与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当
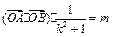 ,且满足2≤m≤4时,
,且满足2≤m≤4时,求△AOB面积的取值范围.
(Ⅰ) b2 = 2(k2 + 1)(k≠±1) (Ⅱ) 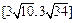
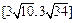
(Ⅰ)因为圆O的方程为x2 + y2 = 2,所以d =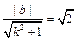 ,可得b2 = 2(k2 + 1)(k≠±1).-------(4分)
,可得b2 = 2(k2 + 1)(k≠±1).-------(4分)
(Ⅱ)设A(x1,y1),B(x2,y2),由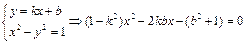 ,
,
所以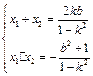 ,--(6分)
,--(6分)
所以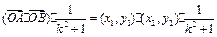 =
=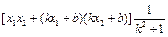
=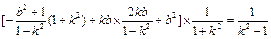 ,
,
因为|AB| =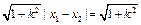 ×
×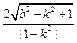 =
=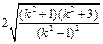 ,
,
O到AB的距离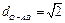 ,------(10分)
,------(10分)
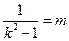 所以
所以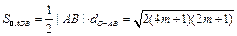
=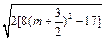 ∈
∈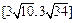 .-----(12分)
.-----(12分)
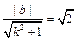 ,可得b2 = 2(k2 + 1)(k≠±1).-------(4分)
,可得b2 = 2(k2 + 1)(k≠±1).-------(4分)(Ⅱ)设A(x1,y1),B(x2,y2),由
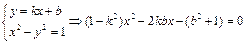 ,
,所以
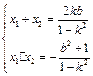 ,--(6分)
,--(6分)所以
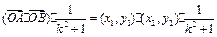 =
=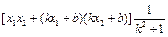
=
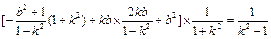 ,
,因为|AB| =
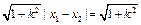 ×
×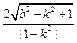 =
=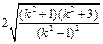 ,
,O到AB的距离
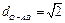 ,------(10分)
,------(10分)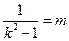 所以
所以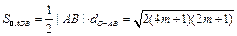
=
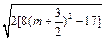 ∈
∈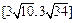 .-----(12分)
.-----(12分)
练习册系列答案
相关题目
 ,定点
,定点 ,问过
,问过 点的直线的斜角在什么范围内取值时,这条直线与圆:(1)相切,(2)相交,(3)相离,并写出过
点的直线的斜角在什么范围内取值时,这条直线与圆:(1)相切,(2)相交,(3)相离,并写出过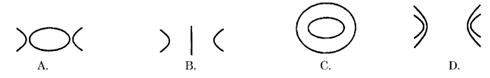
 , BC=
, BC=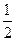 ,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足:
,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足: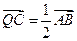 ,问是否存在不平行AB,的直线
,问是否存在不平行AB,的直线 与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线
与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.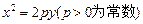 ,
,
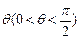 的直线交抛物线于
的直线交抛物线于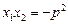
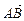 所成的比为
所成的比为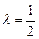 ,求直线AB的方程
,求直线AB的方程 ,求
,求 的函数关系式。
的函数关系式。 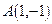
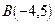
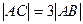
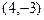 ,B
,B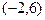 求点C使
求点C使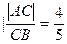 ;
;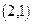 ,F2
,F2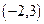 ,离心率e=0.8。求此椭圆长轴上
,离心率e=0.8。求此椭圆长轴上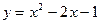
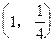
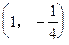
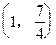
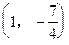
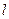 过点(-1,2)且与直线
过点(-1,2)且与直线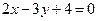 垂直,则
垂直,则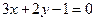 b.
b.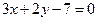
 d.
d.