题目内容
【题目】已知椭圆![]() 和抛物线
和抛物线![]() ,在
,在![]() 上各取两个点,这四个点的坐标为
上各取两个点,这四个点的坐标为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设![]() 是
是![]() 在第一象限上的点,
在第一象限上的点,![]() 在点
在点![]() 处的切线
处的切线![]() 与
与![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,过原点
,过原点![]() 的直线
的直线![]() 与过点
与过点![]() 且垂直于
且垂直于![]() 轴的直线交于点
轴的直线交于点![]() ,证明:点
,证明:点![]() 在定直线上.
在定直线上.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】分析:(Ⅰ)根据椭圆及抛物线的性质可得点![]() ,
,![]() 在椭圆
在椭圆![]() 上,点
上,点![]() ,
, ![]() 在抛物线
在抛物线![]() 上,分别代入求值,即可求得
上,分别代入求值,即可求得![]() 的方程;(Ⅱ)设
的方程;(Ⅱ)设![]() (
(![]() ),根据导数的几何意义可求出切线
),根据导数的几何意义可求出切线![]() 的方程,再设
的方程,再设![]() ,
,![]() ,联立直线
,联立直线![]() 与椭圆的方程,结合韦达定理及线段
与椭圆的方程,结合韦达定理及线段![]() 的中点为
的中点为![]() ,可得
,可得![]() 点坐标,即可表示出直线
点坐标,即可表示出直线![]() 的方程,从而可得点
的方程,从而可得点![]() 在定直线上
在定直线上
详解:(Ⅰ)由已知, 点![]() ,
,![]() 在椭圆
在椭圆![]() 上,所以
上,所以 ![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,所以
,所以![]() :
:![]() ;
;
点![]() ,
, ![]() 在抛物线
在抛物线![]() 上,所以
上,所以![]() ,所以
,所以![]() :
:![]() .
.
(Ⅱ)设![]() (
(![]() ),由
),由![]() 得
得![]() ,所以切线
,所以切线![]() 的方程为:
的方程为:![]() .
.
设![]() ,
,![]() ,由
,由 得:
得:![]() ,
,
由![]() ,
,![]() 得
得![]() ,代入
,代入![]() 得
得![]() .
.
∴![]()
∴![]() :
:![]()
由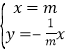 得
得![]() ,所以点
,所以点![]() 在定直线
在定直线![]() 上.
上.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某区组织部为了了解全区科级干部“党风廉政知识”的学习情况,按照分层抽样的方法,从全区320名正科级干部和1280名副科级干部中抽取40名科级干部预测全区科级干部“党风廉政知识”的学习情况.现将这40名科级干部分为正科级干部组和副科级干部组,利用同一份试卷分别进行预测.经过预测后,两组各自将预测成绩统计分析如下表:
分组 | 人数 | 平均成绩 | 标准差 |
正科级干部组 |
| 80 | 6 |
副科级干部组 |
| 70 | 4 |
(1)求![]() ;
;
(2)求这40名科级干部预测成绩的平均分![]() 和标准差
和标准差![]() ;
;
(3)假设该区科级干部的“党风廉政知识”预测成绩服从正态分布![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() .利用估计值估计:该区科级干部“党风廉政知识”预测成绩小于60分的约为多少人?
.利用估计值估计:该区科级干部“党风廉政知识”预测成绩小于60分的约为多少人?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ;
;![]() ;
;![]() .
.