题目内容
【题目】已知函数 和
和![]() (
(![]() 且为常数),则下列结论正确的是( )
且为常数),则下列结论正确的是( )
A.当![]() 时,存在实数
时,存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有四个不同的实数根
有四个不同的实数根
B.存在![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有三个不同的实数根
有三个不同的实数根
C.当![]() 时,若函数
时,若函数![]() 恰有
恰有![]() 个不同的零点
个不同的零点![]() 、
、![]() 、
、![]() ,则
,则![]()
D.当![]() 时,且关于
时,且关于![]() 的方程
的方程![]() 有四个不同的实数根
有四个不同的实数根![]() 、
、![]() 、
、![]() 、
、![]()
![]() ,若
,若![]() 在
在![]() 上的最大值为
上的最大值为![]() ,则
,则![]()
【答案】ACD
【解析】
分![]() 和
和![]() 两种情况讨论,利用数形结合思想可判断出A、B选项的正误;设
两种情况讨论,利用数形结合思想可判断出A、B选项的正误;设![]() ,利用复合函数的零点可判断C选项的正误;求出
,利用复合函数的零点可判断C选项的正误;求出![]() 、
、![]() 的值,结合对称性可判断出D选项的正误.
的值,结合对称性可判断出D选项的正误.
若![]() ,则函数
,则函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
且当![]() 时,
时,![]() ,如下图所示:
,如下图所示:
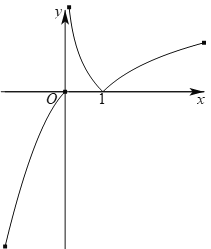
如上图可知,此时关于![]() 的方程
的方程![]() 根的个数不大于
根的个数不大于![]() ,B选项不合乎题意;
,B选项不合乎题意;
若![]() ,且当
,且当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,此时
上单调递减,此时![]() ,
,
当![]() 时,若关于
时,若关于![]() 的方程
的方程![]() 有四个不同的实数根,则
有四个不同的实数根,则![]() ,解得
,解得![]() ,A选项正确;
,A选项正确;
设![]() ,由
,由![]() ,得
,得![]() ,
,
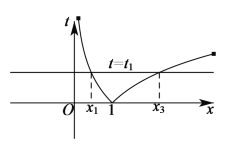
当![]() 时,
时,![]() ,设关于
,设关于![]() 的一元二次方程
的一元二次方程![]() 的两根分别为
的两根分别为![]() 、
、![]() ,由于函数
,由于函数![]() 有三个零点,则
有三个零点,则![]() ,
,![]() ,设
,设![]() ,
,
由![]() ,得
,得![]() ,由图象可知,
,由图象可知,![]() ,
,
由![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,
,![]() ,C选项正确;
,C选项正确;
当![]() 时,若
时,若![]() ,
,![]() ,
,
此时,函数![]() 与函数
与函数![]() 在区间
在区间![]() 上的两个交点关于直线
上的两个交点关于直线![]() 对称,则
对称,则![]() .
.
如下图所示,当![]() 时,函数
时,函数![]() 与函数
与函数![]() 的两个交点的横坐标
的两个交点的横坐标![]() 、
、![]() 满足
满足![]() ,且有
,且有![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,由图象可知,函数
,由图象可知,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调增,
上单调增,![]() ,
,![]() ,
,
所以,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
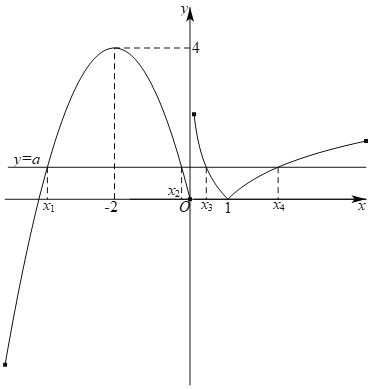
所以,![]() ,D选项正确.
,D选项正确.
故选:ACD.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
