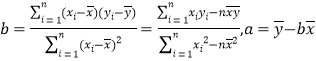题目内容
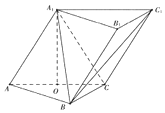
【题目】如图,已知在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() =60°,沿
=60°,沿![]() ,
,![]() 折成三棱柱
折成三棱柱![]() .
.

(1)若![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:
的中点,求证:![]() ∥平面
∥平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
【答案】(1)见解析;(2)![]()
【解析】
分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,在三角形
,在三角形![]() 中,得到
中,得到![]() ,证得
,证得![]() 平面
平面![]() ,又由
,又由![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点证得
的中点证得![]() 平面
平面![]() ,即可证得面
,即可证得面![]() 平面
平面![]() ,利用面面平行的性质,即可得到
,利用面面平行的性质,即可得到![]() 平面
平面![]() .
.
(2)建立如图所示的空间直角坐标系,求得平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解二面角
的法向量,利用向量的夹角公式,即可求解二面角![]() 的余弦值.
的余弦值.
详解:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,在三角形
,在三角形![]() 中,
中,
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
由于![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,由棱柱的性质可得
的中点,由棱柱的性质可得![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴平面![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)连接![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,又
,又![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .
.
建立如图所示的空间直角坐标系,
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则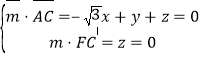 ,则
,则![]() ,令
,令![]() ,
,
得![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,则
,则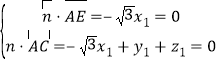 ,
,
则![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设![]() ,
,![]() 所成角为
所成角为![]() ,则
,则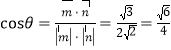 ,
,
由图可知二面角![]() 的余弦值为
的余弦值为![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
相关公式: