题目内容
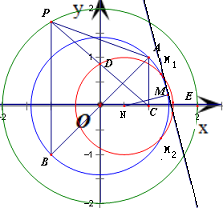
在平面直角坐标系中,A点坐标为(1,1),B点与A点关于坐标原点对称,过动点P作x轴的垂线,垂足为C点,而点D满足2
=
,且有
•
=2,
(1)求点D的轨迹方程;
(2)求△ABD面积的最大值;
(3)斜率为k的直线l被(1)中轨迹所截弦的中点为M,若∠AMB为直角,求k的取值范围.
| PD |
| PC |
| PA |
| PB |
(1)求点D的轨迹方程;
(2)求△ABD面积的最大值;
(3)斜率为k的直线l被(1)中轨迹所截弦的中点为M,若∠AMB为直角,求k的取值范围.
(1)设P(x',y'),得
=(1-x',1-y'),
=(-1-x',-1-y'),
所以
•
=(1-x')(-1-x')+(1-y')(-1-y')=(x')2+(y')2-2
∵
•
=2,
∴点P的轨迹方程为(x')2+(y')2-2=2,即(x')2+(y')2=4…(*)
再设D(x',y'),由2
=
得D为PC的中点
∴x=
(x′+1),y'=
y′.
可得x'=2x-1,y'=2y.代入(*)式得(2x-1)2+(2y)2=4
化简得点D的轨迹方程:(x-
)2+y2=1
(2)设点D坐标为(
+cosα,sinα),
求得直线AB的方程为x-y=0,得D到直线AB的距离为
d=
=
当α=
时,d的最大值为1+
,
因此△ABD面积的最大值为
×AB×(1+
)=1+
;
(3)若∠AMB为直角,则点M在以AB为直径的圆上
求得以AB为直径的圆方程为x2+y2=2,该圆与D的轨迹交于点M1(
,
)和M2(
,-
)
满足条件的点M位于圆N:(x-
)2+y2=1在x2+y2=2内的劣弧上
∵KNM1=
=
,得此时切线l的斜率k1=
=-
KNM2=
=-
,得此时切线l的斜率k2=
=
∴运动点M,观察斜率变化,可得直线l的斜率为k∈(-∞,-
)∪(
,+∞)
| PA |
| PB |
所以
| PA |
| PB |
∵
| PA |
| PB |
∴点P的轨迹方程为(x')2+(y')2-2=2,即(x')2+(y')2=4…(*)
再设D(x',y'),由2
| PD |
| PC |
∴x=
| 1 |
| 2 |
| 1 |
| 2 |
可得x'=2x-1,y'=2y.代入(*)式得(2x-1)2+(2y)2=4
化简得点D的轨迹方程:(x-
| 1 |
| 2 |
(2)设点D坐标为(
| 1 |
| 2 |
求得直线AB的方程为x-y=0,得D到直线AB的距离为
d=
|
| ||
|
|
| ||||||
|
当α=
| 7π |
| 4 |
| ||
| 2 |
因此△ABD面积的最大值为
| 1 |
| 2 |
| ||
| 2 |
| 2 |
(3)若∠AMB为直角,则点M在以AB为直径的圆上
求得以AB为直径的圆方程为x2+y2=2,该圆与D的轨迹交于点M1(
| 5 |
| 4 |
| ||
| 4 |
| 5 |
| 4 |
| ||
| 4 |
满足条件的点M位于圆N:(x-
| 1 |
| 2 |
∵KNM1=
| ||||
|
| ||
| 3 |
| 1 |
| KNM1 |
3
| ||
| 7 |
KNM2=
-
| ||||
|
| ||
| 3 |
| 1 |
| KNM2 |
3
| ||
| 7 |
∴运动点M,观察斜率变化,可得直线l的斜率为k∈(-∞,-
3
| ||
| 7 |
3
| ||
| 7 |


练习册系列答案
相关题目



