题目内容
已知圆C:x2+y2+2x-4y+3=0
(1)求圆心C的坐标及半径r的大小;
(2)已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线的方程.
(1)求圆心C的坐标及半径r的大小;
(2)已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线的方程.
考点:圆的切线方程,圆的一般方程
专题:直线与圆
分析:(1)把圆C的方程化为标准方程,求出圆心C与半径;
(2)设出直线l的方程,由题意,d=r,求出圆的切线方程.
(2)设出直线l的方程,由题意,d=r,求出圆的切线方程.
解答:
解:(1)∵圆C的方程可化为:(x+1)2+(y-2)2=2,
∴圆心C的坐标为(-1,2),半径r=
;…(4分)
(2)∵与圆C相切的直线l不过原点,且在x轴、y轴上的截距相等,
∴设直线l的方程为x+y=a,…(7分)
依题意,d=r,
即
=
;
解得a=-1或a=3,…(12分)
∴所求的切线方程为x+y+1=0或x+y-3=0.…(14分)
∴圆心C的坐标为(-1,2),半径r=
| 2 |
(2)∵与圆C相切的直线l不过原点,且在x轴、y轴上的截距相等,
∴设直线l的方程为x+y=a,…(7分)
依题意,d=r,
即
| |-1+2-a| | ||
|
| 2 |
解得a=-1或a=3,…(12分)
∴所求的切线方程为x+y+1=0或x+y-3=0.…(14分)
点评:本题考查了直线与圆的应用问题,也考查了圆的标准方程与一般方程的互化问题,考查了圆的切线方程问题,是基础题.

练习册系列答案
相关题目
已知f(x)=ax2+bx+c,且b>0,若对任意x有f(x)≥0,则
的最小值为( )
| f(1) |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
若数列{an}的通项公式为an=
,其前n项和为
,则n为( )
| 1 |
| (n+1)(n+2) |
| 7 |
| 18 |
| A、5 | B、6 | C、7 | D、8 |
如果(3x+2)5=a0x5+a1x4+a2x3+a3x2+a4x+a5,那么a0-a1+a2-a3+a4的值等于( )
| A、33 | ||
| B、-31 | ||
C、
| ||
D、
|
直线l:kx+(1-k)y-3=0经过的定点是( )
| A、(0,1) |
| B、(3,3) |
| C、(1,-3) |
| D、(1,1) |
设a=
(3x2-2x)dx,则a=( )
| ∫ | 2 1 |
| A、12 | B、4 | C、-12 | D、-4 |
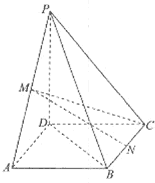 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M、N分别为PA、BC的中点,且PD=AD=1,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M、N分别为PA、BC的中点,且PD=AD=1,