题目内容
函数f(x)=a x2-(a+1)x+2在区间(-∞,1)上是减函数,那么实数a的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:a=0时,函数f(x)=-x+2为一次函数,显然满足在(-∞,1)上是减函数;a≠0时,函数f(x)为二次函数,根据二次函数的单调性即可求得a的取值范围,合并这两种情况即得实数a的取值范围.
解答:
解:①a=0时,f(x)=-x+2,该函数为一次函数,在(-∞,1)上是减函数;
②若a≠0,函数f(x)为二次函数,对称轴为x=
;
要使f(x)在区间(-∞,1)上是减函数,则:
,解得0<a≤1;
综上得a的取值范围为[0,1].
故答案为:[0,1].
②若a≠0,函数f(x)为二次函数,对称轴为x=
| a+1 |
| 2a |
要使f(x)在区间(-∞,1)上是减函数,则:
|
综上得a的取值范围为[0,1].
故答案为:[0,1].
点评:考查一次函数的单调性,以及二次函数单调性和对称轴的关系,不要漏了a=0的情况.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
数列{an}中,an=
,则前n和Sn等于( )
| 2 |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
若sinx•cosx=
,且
<x<
,则cosx-sinx的值是( )
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、±
|
直线3x-4y+1=0被圆(x-3)2+y2=9截得的弦长为( )
A、
| ||
| B、4 | ||
C、2
| ||
| D、2 |
若a>b>0,则下列结论正确的是( )
| A、a2<b2 | ||
| B、ab<b2 | ||
C、a+b>2
| ||
| D、a-b>a+b |
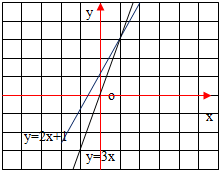 在同一坐标系中作出y=2x+1,y=3x的图象.
在同一坐标系中作出y=2x+1,y=3x的图象.