题目内容
17.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,下顶点和上顶点分别为B1,B2,以B1为圆心,B1B2为半径的圆恰好经过点F且与直线3x-4y+6=0相切,求椭圆C的方程.分析 利用已知条件列出方程组,求出椭圆的几何量,即可求解椭圆的方程.
解答 解:设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,下顶点和上顶点分别为B1(0,b),B2(0,-b),以B1为圆心,B1B2为半径的圆恰好经过点F且与直线3x-4y+6=0相切,
可得:2b=a,$\frac{|-4b+6|}{\sqrt{{3}^{2}+({-4)}^{2}}}=2b$,
解得:b=$\frac{3}{7}$,a=$\frac{6}{7}$,
所求椭圆方程为:$\frac{49{x}^{2}}{9}+\frac{49{y}^{2}}{36}=1$.
故答案为:$\frac{49{x}^{2}}{9}+\frac{49{y}^{2}}{36}=1$.
点评 本题考查椭圆的简单性质的应用,考查椭圆的方程以及直线与圆的位置关系,考查计算能力.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
7.函数y=(2x-1)ex的图象是( )
| A. |  | B. |  | C. |  | D. |  |
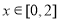 时,函数
时,函数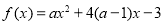 在
在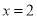 时取得最大值,则
时取得最大值,则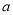 的取值范围是( )
的取值范围是( )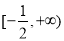 B.
B.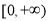
 D.
D.