题目内容
17. 如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.
如图,在直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+m(m为常数)的图象与x轴交于A(-3,0),与y轴交于点C.以直线x=-1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A、C两点,与x轴正半轴交于点B.(1)求一次函数及抛物线的函数表达式.
(2)已知在对称轴上是否存在一点P,使得△PBC的周长最小,若存在,请求出点P的坐标.
(3)点D是线段OC上的一个动点(不与点O、点C重合),过点D作DE‖PC交x轴于点E,连接PD、PE.设CD的长为m,△PDE的面积为S.求S与m之间的函数关系式.并说明S是否存在最大值,若存在,请求出最大值:若不存在,请说明理由.
分析 (1)运用代入法,可得直线AC的方程;设抛物线的方程为y=a(x+3)(x-1),代入点(0,-2),即可得到抛物线方程;
(2)要使△PBC周长最大,只需BP+CP最小即可,由轴对称性质以及两点间线段最短,可知此时BP+CP最小;
(3)运用三角形的面积公式和割补法,可得S,m的关系式,结合二次函数的最值求法,即可得到最大值.
解答 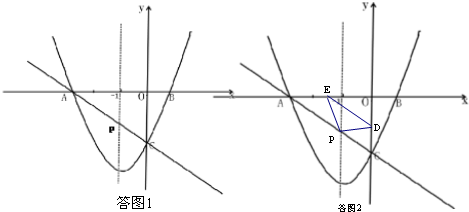 解:(1)y=-$\frac{2}{3}$x+m过点A(-3,0),
解:(1)y=-$\frac{2}{3}$x+m过点A(-3,0),
则m+2=0,解得m=-2,
则直线AC:y=-$\frac{2}{3}$x-2;
由C(0,-2),
抛物线y=ax2+bx+c的对称轴为x=-1,
且与x轴交于A(-3,0),另一交点为B(1,0),
设抛物线的方程为y=a(x+3)(x-1),
代入点(0,-2),可得a=$\frac{2}{3}$,
即有抛物线的方程为y=$\frac{2}{3}$x2+$\frac{4}{3}$x-2;
(2)要使△PBC周长最大,只需BP+CP最小即可,如图1,
连AC交x=-1于P点,由A,B关于直线x=-1对称,
由轴对称性质以及两点间线段最短,可知此时BP+CP最小,
(BP+CP最小即为AC的长),
由A(-3,0),C(0,-2),AC:y=-$\frac{2}{3}$x-2,
由xP=-1,则yP=-$\frac{4}{3}$,P(-1,-$\frac{4}{3}$);
(3)如图2,设CD=m,△PDE的面积为S,D(0,m-2),
DE∥PC,AC:y=-$\frac{2}{3}$x-2,设DE:y=-$\frac{2}{3}$x+m-2,
当y=0时,x=$\frac{3}{2}$m-3,即D($\frac{3}{2}$m-3,0),
S△PDE=S△AOC-S△DOE-S△PDC-S△PEA
=3-$\frac{1}{2}$•$\frac{3}{2}$m•$\frac{4}{3}$-$\frac{1}{2}$(3-$\frac{3}{2}$m)(2-m)-$\frac{1}{2}$m•1=-$\frac{3}{4}$m2+$\frac{3}{2}$m
=-$\frac{3}{4}$(m-1)2+$\frac{3}{4}$,
当m=1时,取得最大值,且为$\frac{3}{4}$.
点评 本题考查抛物线的方程和性质,主要考查抛物线的方程的求法,同时考查三角形的周长的最小和面积的最大,注意运用对称性和二次函数的最值求法是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | b<a<c |
| A. | -ln(-x)+1 | B. | ln(-x)+1 | C. | -ln(-x)-1 | D. | ln(-x)-1 |