题目内容
【题目】已知函数![]() 曲线
曲线![]() 在原点处的切线为
在原点处的切线为![]() .
.
(1)证明:曲线![]() 与
与![]() 轴正半轴有交点;
轴正半轴有交点;
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,曲线在点
,曲线在点![]() 处的切线为直线
处的切线为直线![]() ,求证:曲线
,求证:曲线![]() 上的点都不在直线
上的点都不在直线![]() 的上方 ;
的上方 ;
(3)若关于![]() 的方程
的方程![]() (
(![]() 为正实数)有不等实根
为正实数)有不等实根![]() 求证:
求证:![]()
【答案】(1)见解析(2)见解析(3)见解析
【解析】分析:(1)由条件可得![]() ,然后利用单调性及零点存在定理可得存在
,然后利用单调性及零点存在定理可得存在![]() 使得
使得![]() ,从而得结论成立.(2)由(1)可得曲线
,从而得结论成立.(2)由(1)可得曲线![]() 在点
在点![]() 处的切线
处的切线![]() :
:![]() . 令
. 令![]() ,
,![]() ,则
,则![]() ,由
,由![]() 的单调性可得
的单调性可得![]() ,从而可得结论成立.(3)结合以上两问中的有关结论构造新的函数进行证明可得结论成立.
,从而可得结论成立.(3)结合以上两问中的有关结论构造新的函数进行证明可得结论成立.
详解:证明:(1)∵![]() ,
,
∴![]() ,
,
由已知得![]() ,解得
,解得![]()
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又![]() ,
,![]() ,
,
∴存在![]() 使得
使得![]() .
.
∴曲线![]() 与
与![]() 轴正半轴有交点
轴正半轴有交点![]() .
.
(2)由(1)可得曲线![]() 在点
在点![]() 处的切线
处的切线![]() :
:![]() ,
,
令![]() ,
,![]() ,
,
则![]() ,
,
又![]() ,
,
故当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以对任意实数![]() 都有
都有![]() ,
,
即对任意实数![]() 都有
都有![]() ,
,
故曲线![]() 上的点都不在直线
上的点都不在直线![]() 的上方.
的上方.
(3)由(1)知![]() ,
,
所以![]() 为减函数.
为减函数.
设方程![]() 的根为
的根为![]() ,
,
由(2)可知![]() ,
,
所以![]() .
.
记![]() ,则
,则![]()
当![]() 时,
时,![]()
![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,单调递减,
,单调递减,
所以对任意的实数![]() ,都有
,都有![]() ,
,
即![]() .
.
设方程![]() 的根
的根![]() ,
,
则![]() ,
,
所以![]() .
.
于是![]()
令![]() ,
,
又![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上为增函数,
上为增函数,
又![]()
所以![]() ,
,
所以![]()

【题目】一只药用昆虫的产卵数![]() 与一定范围内与温度
与一定范围内与温度![]() 有关, 现收集了该种药用昆虫的6组观测数据如下表:
有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求![]() 关
关![]() 的回归方程为
的回归方程为![]()
![]() 且相关指数
且相关指数![]()
( i )试与 (1)中的线性回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为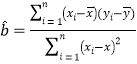 ,
,![]() ,相关指数
,相关指数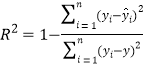 .
.
![]()
![]()
![]()
![]() 。
。