题目内容
【题目】设函数![]() ,
, ![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,讨论函数
时,讨论函数![]() 与
与![]() 的图象的交点个数.
的图象的交点个数.
【答案】(1)当![]() 时,函数
时,函数![]() 的单调增区间是
的单调增区间是![]() ,无减区间,当
,无减区间,当![]() 时,函数
时,函数![]() 的单调增区间是
的单调增区间是![]() ,减区间是
,减区间是![]() ;(2)两函数图象总有一个交点.
;(2)两函数图象总有一个交点.
【解析】试题分析:(1)在定义域的前提下对函数求导,对![]() 分类:
分类: ![]() ,
, ![]() .可函数的单调区间;(2)设
.可函数的单调区间;(2)设![]() ,本题可转化为求
,本题可转化为求![]() 的零点个数问题,对
的零点个数问题,对![]() 分类讨论即可.
分类讨论即可.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 的单调增区间是
的单调增区间是![]() ,无减区间;
,无减区间;
当![]() 时,
时, 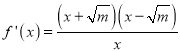 ;当
;当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增.
单调递增.
综上,当![]() 时,函数
时,函数![]() 的单调增区间是
的单调增区间是![]() ,无减区间;
,无减区间;
当![]() 时,函数
时,函数![]() 的单调增区间是
的单调增区间是![]() ,减区间是
,减区间是![]() .
.
(2)解:令![]() ,
, ![]() ,问题等价于求函数
,问题等价于求函数![]() 的零点个数.
的零点个数.
当![]() 时,
时, ![]() ,
, ![]() ,有唯一零点;
,有唯一零点;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ,函数
,函数![]() 为减函数,注意到
为减函数,注意到![]() ,
, ![]() ,所以
,所以![]() 有唯一零点;
有唯一零点;
当![]() 时,
时, ![]() 或
或![]() 时,
时, ![]() ,
, ![]() 时
时![]() ,所以函数
,所以函数![]() 在
在![]() 和
和![]() 单调递减,在
单调递减,在![]() 单调递增,注意到
单调递增,注意到![]() ,
, ![]() ,所以
,所以![]() 有唯一零点;
有唯一零点;
当![]() 时,
时, ![]() 或
或![]() 时
时![]() ,
, ![]() 时
时![]() ,所以函数
,所以函数![]() 在
在![]() 和
和![]() 单调递减,在
单调递减,在![]() 单调递增,注意到
单调递增,注意到![]() ,所以
,所以![]() ,而
,而![]() ,所以
,所以![]() 有唯一零点.
有唯一零点.
综上,函数![]() 有唯一零点,即两函数图象总有一个交点.
有唯一零点,即两函数图象总有一个交点.

练习册系列答案
相关题目