题目内容
若抛物线y2=4x的焦点是F准线是l,则过点F和点M(4,4)且与准线l相切的圆有( )
| A.0个 | B.1个 | C.2个 | D.4个 |
C
:抛物线y2=4x的焦参数p=2,所以F(1,0),直线l:x=-1,即x+1=0,
设经过点M(4,4)、F(1,0),且与直线l相切的圆的圆心为Q(g,h),
则半径为Q到,l的距离,即1+g,所以圆的方程为(x-g)2+(y-h)2=(1+g)2,
将M、F的坐标代入,得(4-g)2+(4-h)2=(1+g)2,(1-g)2+(0-h)2=(1+g)2,
即h2-8h+1=10g①,
h2=4g②,②代入①,
得3h2+16h-2=0,解得h有两个解,那恶魔对应的g有两解,因此圆有2个,选C
设经过点M(4,4)、F(1,0),且与直线l相切的圆的圆心为Q(g,h),
则半径为Q到,l的距离,即1+g,所以圆的方程为(x-g)2+(y-h)2=(1+g)2,
将M、F的坐标代入,得(4-g)2+(4-h)2=(1+g)2,(1-g)2+(0-h)2=(1+g)2,
即h2-8h+1=10g①,
h2=4g②,②代入①,
得3h2+16h-2=0,解得h有两个解,那恶魔对应的g有两解,因此圆有2个,选C

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
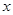 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点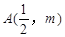 ,
,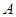 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设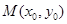 为抛物线上的一个定点,过
为抛物线上的一个定点,过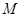 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦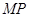 ,
,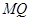 ,求证:
,求证: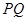 恒过定点
恒过定点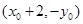 .(3)直线
.(3)直线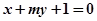 与抛物线交于
与抛物线交于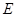 ,
,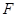 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点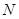 ,使得△
,使得△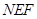 为以
为以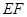 为斜边的直角三角形.
为斜边的直角三角形.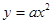 的焦点坐标为
的焦点坐标为
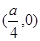
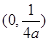

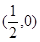 的距离与P到直线
的距离与P到直线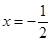 距离相等
距离相等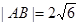 ,求直线l的方程;
,求直线l的方程;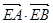 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.  上一点
上一点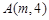 到其焦点的距离为
到其焦点的距离为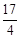 ,则m= .
,则m= .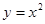 上的点M(
上的点M(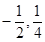 )的切线的倾斜角为( )
)的切线的倾斜角为( )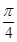
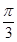

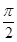
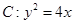 ,过点
,过点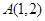 作抛物线
作抛物线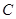 的弦
的弦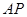 ,
,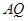 .
.
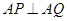 ,证明直线
,证明直线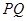 过定点,并求出定点的坐标;
过定点,并求出定点的坐标;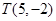 ,请问是否存在以
,请问是否存在以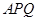 ? 若存在,求出
? 若存在,求出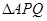 的个数?如果不存在,请说明理由.
的个数?如果不存在,请说明理由.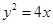 的准线为
的准线为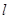 ,
,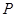 为抛物线上的点,
为抛物线上的点,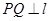 ,垂足为
,垂足为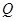 ,若
,若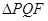 得面积与
得面积与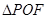 的面积之比为
的面积之比为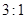 ,则
,则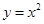 与直线
与直线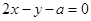 相切,则
相切,则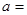 ________
________