题目内容
等轴双曲线 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 与抛物线
与抛物线 的准线交于
的准线交于 两点,
两点, ;则
;则 的实轴长为
的实轴长为
A. | B. | C.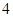 | D. |
C
解析试题分析:因为双曲线C是等轴双曲线,且焦点在x轴上,所以设C的方程为: ,
,
因为抛物线的准线为x=-4,把x=-4代入双曲线方程得: ,因为
,因为 ,所以
,所以 ,所以m=4.所以C的方程为:
,所以m=4.所以C的方程为: ,所以
,所以 的实轴长为4.
的实轴长为4.
考点:本题考查双曲线的简单性质;抛物线的简单性质;双曲线与抛物线的综合应用。
点评:本题考查双曲线与抛物线的性质和应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
抛物线 上一点
上一点 到焦点的距离为1,则点
到焦点的距离为1,则点 的纵坐标是 ( )
的纵坐标是 ( )
| A.0 | B. | C. | D. |
已知抛物线 ,其焦点坐标是( )
,其焦点坐标是( )
A. | B. | C. | D. |
椭圆 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则m的值为 ( )
轴上,长轴长是短轴长的两倍,则m的值为 ( )
A. | B. | C. | D. |
曲线 与曲线
与曲线 的( )
的( )
| A.长轴长相等 | B.短轴长相等 | C.离心率相等 | D.焦距相等 |

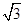


 、
、 是双曲线
是双曲线 的两焦点,点
的两焦点,点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,则
是等腰三角形,则



 和双曲线
和双曲线 的公共焦点为
的公共焦点为 、
、  ,
, 是两曲线的一个交点,那么
是两曲线的一个交点,那么 的值是 ( )
的值是 ( )



 的两个焦点,过F2的直线交椭圆于点A、B,若
的两个焦点,过F2的直线交椭圆于点A、B,若 ,
,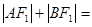 ( )
( )