题目内容
椭圆 的两焦点为
的两焦点为 、
、 ,以
,以 为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )
为边作正三角形,若椭圆恰好平分该正三角形的另两边,则椭圆的离心率是( )
A. | B. | C. | D. |
D
解析试题分析:以 为边作正三角形,则三角形的第三个顶点一定在y轴上,又因为椭圆恰好平分该正三角形的另两边,所以另外两边的中点在椭圆上,因为
为边作正三角形,则三角形的第三个顶点一定在y轴上,又因为椭圆恰好平分该正三角形的另两边,所以另外两边的中点在椭圆上,因为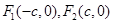 ,不妨设第三个顶点在y轴的正半轴上,则第三个顶点的坐标为
,不妨设第三个顶点在y轴的正半轴上,则第三个顶点的坐标为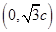 ,所以中点
,所以中点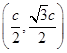 在椭圆上,代入椭圆方程得:
在椭圆上,代入椭圆方程得: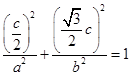 ,又因为
,又因为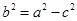 ,可以得到离心率为
,可以得到离心率为 .
.
考点:本小题主要考查椭圆上点的性质和椭圆的离心率的求法,考查学生的运算求解能力.
点评:求椭圆的离心率,只要把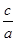 求出来就可以了,不必把
求出来就可以了,不必把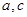 分别求出来.
分别求出来.

练习册系列答案
相关题目
椭圆上 一动点P到两焦点距离之和为( )
一动点P到两焦点距离之和为( )
| A.10 | B.8 | C.6 | D.不确定 |
已知抛物线 ,其焦点坐标是( )
,其焦点坐标是( )
A. | B. | C. | D. |
双曲线 的实轴长是
的实轴长是
| A.2 | B. | C.4 | D.4 |
设直线 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 与椭圆
与椭圆 的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为
的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为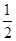 的点M的个数为
的点M的个数为
| A.1 | B.2 | C.3 | D.4 |
 上一点
上一点 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线 的左顶点为
的左顶点为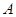 ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线 平行,则实数
平行,则实数 的值是( )
的值是( )



 (a>0,b>0)的一条渐近线方程是y=
(a>0,b>0)的一条渐近线方程是y= x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )



 和双曲线
和双曲线 的公共焦点为
的公共焦点为 、
、  ,
, 是两曲线的一个交点,那么
是两曲线的一个交点,那么 的值是 ( )
的值是 ( )



 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: .给出下列三个命题:
.给出下列三个命题: ;
; 中,若∠C=90°,则
中,若∠C=90°,则 ;
; .
.