题目内容
7.已知函数f(x)=ax3+bx2-3x(a,b∈R)的图象在点(1,-2)处切线斜率为0.(1)求a,b的值;
(2)若对于区间[-2,2]上任意自变量的x0,都有|f(x0)|≤c,求实数c的最小值.
分析 (1)由题意,利用导函数的几何含义及切点的实质建立a,b的方程,然后求解即可;
(2)由题意,若对于区间[-2,2]上任意自变量的x0,都有|f(x0)|≤c,可以转化为求函数在定义域下的最值即可得解.
解答 解:(1)f′(x)=3ax2+2bx-3.
根据题意,得$\left\{\begin{array}{l}{f(1)=-2}\\{f′(1)=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a+b-3=-2}\\{3a+2b-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$,
所以f(x)=x3-3x;
(2)令f′(x)=0,即3x2-3=0.得x=±1.
当x∈(-∞,-1)时,f′(x)>0,函数f(x)在此区间单调递增;
当x∈(-1,1)时,f′(x)<0,函数f(x)在此区间单调递减.
因为f(-1)=2,f(1)=-2,
所以当x∈[-2,2]时,f(x)max=2,f(x)min=-2.
若对于区间[-2,2]上任意自变量的x0,都有|f(x0)|≤c,所以c≥2.
所以c的最小值为2.
点评 此题重点考查了导数的几何含义及函数切点的定义,还考查了数学中重要的方程的思想,考查了数学中等价转化的思想把题意总转化为求函数在定义域下的最值.

练习册系列答案
相关题目
12.设随机变量ξ的分布列为P(ξ=k)=${C}_{n}^{k}$($\frac{2}{3}$)k($\frac{1}{3}$)n-k,k=0,1,2,…,n,且Eξ=24,则Dξ的值为( )
| A. | 8 | B. | 12 | C. | $\frac{2}{9}$ | D. | 16 |
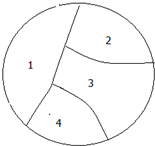 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.