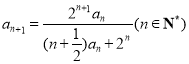题目内容
【题目】已知椭圆
，且椭圆上任意一点到左焦点的最大距离为
，最小距离为
.
（1）求椭圆的方程；
（2）过点
的动直线
交椭圆
于
两点，试问：在坐标平面上是否存在一个定点
，使得以线段
为直径的圆恒过点
?若存在，求出点
的坐标：若不存在，请说明理由.
【答案】(1) 椭圆方程为
;(2) 以线段
为直径的圆恒过点
.
【解析】试题分析：（1）通过椭圆的几何意义得到椭圆的方程；（2）先考虑直线的特殊情况，和轴垂直，和轴平行，通过这两种情况得到最终结果再证明一般情况. 以线段
为直径的圆恒过点
，转化为
，通过韦达定理解决即可。
（1）椭圆方程为
.
（2）当
与
轴平行时，以线段
为直径的圆的方程为
；
当
与
轴平行时，以线段
为直径的圆的方程为
.
故若存在定点
，则
的坐标只可能为
.
下面证明
为所求：
若直线
的斜率不存在，上述己经证明.
若直线
的斜率存在，设直线
， 
，
由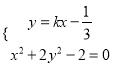
得
，
，
，
， 
.
∴
，即以线段
为直径的圆恒过点
.
期末宝典单元检测分类复习卷系列答案
【题目】某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间(x个月)和市场占有率(y%)的几组相关对应数据：
x | 1 | 2 | 3 | 4 | 5 |
y | 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据，用最小二乘法求出y关于x的线性回归方程；
(2)根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过0.5%(精确到月)．
附： 
， 
.
【题目】某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．
整理评分数据，将分数以
为组距分成
组：
，
，
，
，
，
，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
（Ⅰ）在抽样的100人中，求对A餐厅评分低于30的人数；
（Ⅱ）从对B餐厅评分在
范围内的人中随机选出2人，求2人中恰有1人评分在范围内的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．
