题目内容
12.设函数y=arccos(x2-$\frac{1}{4}$)的最大值α,最小值β,cos[π-(α+β)]=$\frac{1}{4}$.分析 根据x2-$\frac{1}{4}$∈[-$\frac{1}{4}$,1],求得函数的最大值α,最小值β,再利用诱导公式求得cos[π-(α+β)]的值.
解答 解:由x2-$\frac{1}{4}$∈[-$\frac{1}{4}$,1],可得函数y=arccos(x2-$\frac{1}{4}$)的最大值α=arccos(-$\frac{1}{4}$)=π-arccos$\frac{1}{4}$,最小值β=0,
∴cos[π-(α+β)]=-cos(α+β)=-cos[π-arccos$\frac{1}{4}$]=cos(arccos$\frac{1}{4}$)=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 本题主要考查诱导公式、反余弦函数的定义和性质,属于基础题.

练习册系列答案
相关题目
20.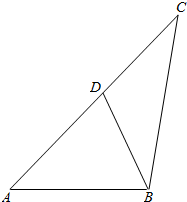 如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )
如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )
 如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )
如图,在△ABC中,AB=2,AC=4,线段CB的垂直平分线交线段AC于D,AD-DB=1,则△BCD的面积为( )| A. | $\frac{7}{10}$ | B. | $\frac{9}{10}$ | C. | 2 | D. | 8 |
1.若等差数列{an}满足a12+a32=2,则$\frac{{{a}_{3}}^{2}+{{a}_{4}}^{2}}{{{a}_{4}}^{2}+{{a}_{5}}^{2}}$的取值范围是( )
| A. | [1,3] | B. | [$\sqrt{5}$-1,$\sqrt{5}$十1] | C. | [3-2$\sqrt{2}$,3+2$\sqrt{2}$] | D. | [4-2$\sqrt{3}$,4+2$\sqrt{3}$]. |