题目内容
已知函数f(x)=Asin(ωx+
)(x∈R,A>0,ω>0)的最小正周期为T=6π,且f(2π)=2
(1)求ω和A的值;
(2)设α,β∈[0,
],f(3α+π)=
,f(3β+
)=-
;求cos(α-β)的值.
| π |
| 6 |
(1)求ω和A的值;
(2)设α,β∈[0,
| π |
| 2 |
| 16 |
| 5 |
| 5π |
| 2 |
| 20 |
| 13 |
(1)依题意得ω=
=
=
,
∴函数f(x)=Asin(
+
)(2分)
由f(2π)=2得Asin(
+
)=2,
即Asin
=2,
∴A=4(4分)
∴函数f(x)=4sin(
+
)(5分)
(2)由f(3α+π)=
,得4sin[
(3α+π)+
]=
,
即4sin(α+
)=
.
∴cosα=
,(6分)
又∵α∈[0,
],∴sinα=
.(7分)
由f(3β+
)=-
得4sin[
(3β+
)+
]=-
,即sin(β+π)=-
,
∴sinβ=
,(9分)
又∵β∈[0,
],
∴cosβ=
(10分)
cos(α-β)=cosαcosβ+sinαsinβ=
×
+
×
=
.(12分)
| 2π |
| T |
| 2π |
| 6π |
| 1 |
| 3 |
∴函数f(x)=Asin(
| x |
| 3 |
| π |
| 6 |
由f(2π)=2得Asin(
| 2π |
| 3 |
| π |
| 6 |
即Asin
| 5π |
| 6 |
∴A=4(4分)
∴函数f(x)=4sin(
| x |
| 3 |
| π |
| 6 |
(2)由f(3α+π)=
| 16 |
| 5 |
| 1 |
| 3 |
| π |
| 6 |
| 16 |
| 5 |
即4sin(α+
| π |
| 2 |
| 16 |
| 5 |
∴cosα=
| 4 |
| 5 |
又∵α∈[0,
| π |
| 2 |
| 3 |
| 5 |
由f(3β+
| 5π |
| 2 |
| 20 |
| 13 |
| 1 |
| 3 |
| 5π |
| 2 |
| π |
| 6 |
| 20 |
| 13 |
| 5 |
| 13 |
∴sinβ=
| 5 |
| 13 |
又∵β∈[0,
| π |
| 2 |
∴cosβ=
| 12 |
| 13 |
cos(α-β)=cosαcosβ+sinαsinβ=
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 63 |
| 65 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


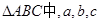 分别是角A、B、C的对边,
分别是角A、B、C的对边,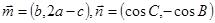 ,且
,且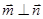 .
. ,
, ,那么
,那么 的值为________ .
的值为________ .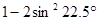 的结果等于______.
的结果等于______.